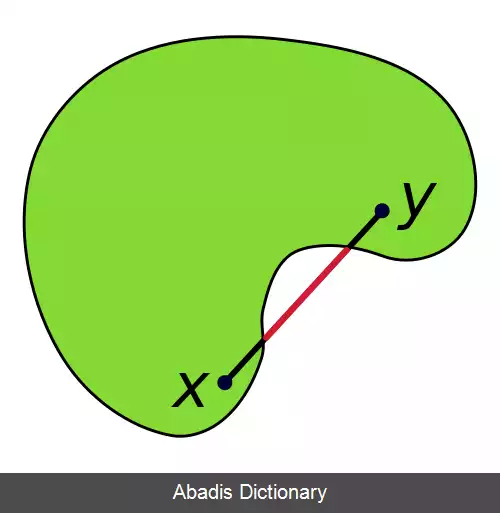
مجموعهٔ کوژ یا مجموعهٔ محدب، زیرمجموعه ای از فضای اقلیدسی است که هر ترکیب محدب از هر دو عضو دلخواه آن عضوش باشد. به بیان دیگر، مجموعه ای را محدب می نامیم، که هر پاره خط واصل دو نقطهٔ دلخواه آن به طور کامل درونش قرار گیرد.
گوییم k ⊂ R n مجموعه ای محدب است، اگر هر ترکیب محدب از هر دو عضو k همچنان عضو k باشد. یعنی اگر x ~ ∈ k و y ^ ∈ k آنگاه به ازای هر 0 ≤ α ≤ 1 داشته باشیم α x ~ + ( 1 − α ) y ^ ∈ k .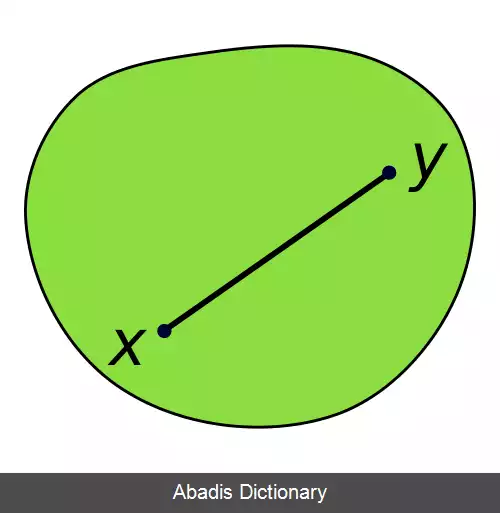
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفگوییم k ⊂ R n مجموعه ای محدب است، اگر هر ترکیب محدب از هر دو عضو k همچنان عضو k باشد. یعنی اگر x ~ ∈ k و y ^ ∈ k آنگاه به ازای هر 0 ≤ α ≤ 1 داشته باشیم α x ~ + ( 1 − α ) y ^ ∈ k .


wiki: مجموعه محدب
