مجموعه جزئی مرتب[ ۱] ( به انگلیسی: partially ordered set ) در ریاضیات و مخصوصاً نظریه ترتیب، «مفهوم شهودی یک ترتیب، پیاپی سازی، یا چینش عناصر یک مجموعه» را صوری سازی می کند و تعمیم می دهد. به مجموعه جزئی مرتب به صورت مخفف، پوسِت ( به انگلیسی: poset ) هم می گویند. یک پوسِت شامل یک «مجموعه» همراه با یک «رابطه دوتایی» است، که این رابطه بیانگر آن است که برای جفت عنصرهای خاصی در آن مجموعه، یکی از آن عناصر از نظر ترتیبی قبل از دیگری قرار دارد. به چنین رابطه ای، «رابطه جزئی مرتب»[ ۱] می گویند.
در اینجا واژه «جزئی» بیانگر آن است که «همه جفت عضوها نیاز به قابل مقایسه بودن ندارند». یعنی ممکن است در یک پوسِت جفت عضوی موجود باشد، که هیچ کدام از آن عناصر قبل از دیگری نیست. در واقع «مجموعه های جزئی مرتب» ویژگی های یک «مجموعه های کاملاً مرتب» ( ترتیب کامل ) را تعمیم می دهد. در مجموعه های کاملاً مرتب، همه جفت عنصرها قابل مقایسه اند.
یک مجموعه ترتیب جزئی یک رابطه باینری "≥" روی مجموعهٔ ( به طور مثال ) P است که خواص بازتابی، تعدی و پادتقارنی داشته باشد.
a ≤ a ( بازتابی ) .
if a ≤ b and b ≤ a, then a = b ( پادتقارنی ) .
if a ≤ b and b ≤ c, then a ≤ c ( تعدی ) .
مجموعه ای که دارای خاصیت ترتیب جزئی باشد را POSet می نامیم. برای اعضا a و b از مجموعهٔ POSet اگر a ≤ b یا b ≤ a آنگاه a و b را قابل قیاس می نامند و در غیر این صورت غیرقابل قیاس. در عکس بالا می توان دید که {x} و {x, y, z} قابل قیاس اند ولی {x} و {y} نیستند.
به مجموعه مرتبی که همه اعضا آن قابل قیاس باشد، ترتیب کامل ( total order یا linear order ) می گوییم. یک ترتیب کلی را زنجیر ( chain ) نیز می نامند.
اگر عنصری همانند g در P باشد. . هنگامی بزرگترین عضو است که به ازای هر a عضو P, a ≤ g و به صورت مشابه برای کوچکترین عضو اگر عنصری همانند m عضو P را در نظر بگیریم m کوچکترین عضو است وقتی به ازای هر a, a ≥ m.
عنصری مانند g از مجموعه p یک عنصر بیشین است. اگر هیچ عنصری همانند a از p نباشد که a> g. به صورت مشابه برای عضو کمین. . عنصری همانند m از P وجود نداشته باشد که g < m. عنصر بیشینه در صورتی وجود دارد که عنصر بیشین یکتا باشد ( کمینه است در صورتی که عنصر کمین بکتا باشد ) .
به صورت مشابه برای کران پایین اگر a ≥ x برای هر عضو a از A. بزرگترین عضو مجموعه ( ترتیب جزئی ) P نیز کران بالا P است؛ و بهصورت مشابه برای کران پایین.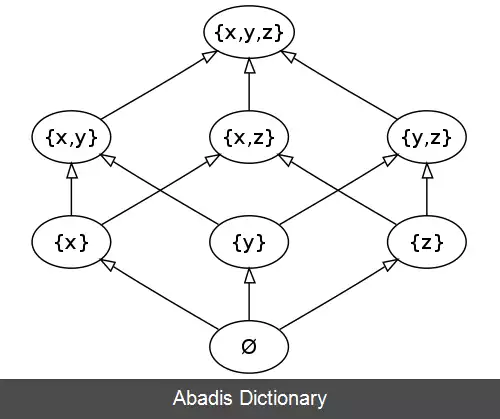
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر اینجا واژه «جزئی» بیانگر آن است که «همه جفت عضوها نیاز به قابل مقایسه بودن ندارند». یعنی ممکن است در یک پوسِت جفت عضوی موجود باشد، که هیچ کدام از آن عناصر قبل از دیگری نیست. در واقع «مجموعه های جزئی مرتب» ویژگی های یک «مجموعه های کاملاً مرتب» ( ترتیب کامل ) را تعمیم می دهد. در مجموعه های کاملاً مرتب، همه جفت عنصرها قابل مقایسه اند.
یک مجموعه ترتیب جزئی یک رابطه باینری "≥" روی مجموعهٔ ( به طور مثال ) P است که خواص بازتابی، تعدی و پادتقارنی داشته باشد.
a ≤ a ( بازتابی ) .
if a ≤ b and b ≤ a, then a = b ( پادتقارنی ) .
if a ≤ b and b ≤ c, then a ≤ c ( تعدی ) .
مجموعه ای که دارای خاصیت ترتیب جزئی باشد را POSet می نامیم. برای اعضا a و b از مجموعهٔ POSet اگر a ≤ b یا b ≤ a آنگاه a و b را قابل قیاس می نامند و در غیر این صورت غیرقابل قیاس. در عکس بالا می توان دید که {x} و {x, y, z} قابل قیاس اند ولی {x} و {y} نیستند.
به مجموعه مرتبی که همه اعضا آن قابل قیاس باشد، ترتیب کامل ( total order یا linear order ) می گوییم. یک ترتیب کلی را زنجیر ( chain ) نیز می نامند.
اگر عنصری همانند g در P باشد. . هنگامی بزرگترین عضو است که به ازای هر a عضو P, a ≤ g و به صورت مشابه برای کوچکترین عضو اگر عنصری همانند m عضو P را در نظر بگیریم m کوچکترین عضو است وقتی به ازای هر a, a ≥ m.
عنصری مانند g از مجموعه p یک عنصر بیشین است. اگر هیچ عنصری همانند a از p نباشد که a> g. به صورت مشابه برای عضو کمین. . عنصری همانند m از P وجود نداشته باشد که g < m. عنصر بیشینه در صورتی وجود دارد که عنصر بیشین یکتا باشد ( کمینه است در صورتی که عنصر کمین بکتا باشد ) .
به صورت مشابه برای کران پایین اگر a ≥ x برای هر عضو a از A. بزرگترین عضو مجموعه ( ترتیب جزئی ) P نیز کران بالا P است؛ و بهصورت مشابه برای کران پایین.

wiki: مجموعه جزئی مرتب
