در آمار کاربردی، مجموع کمترین مربعات، نوعی از خطاهای رگرسیون متغیرها می باشد و به عبارتی دیگر یک تکنیک مدل سازی داده های کمترین مربعات بوده که در آن خطاهای مشاهده شده هم بر روی متغیرهای وابسته و هم بر روی متغیرهای مستقل به دست آوردن می شود. مجموع کمترین مربعات، تعمیمی از رگرسیون دمینک و نیز تعمیمی از رگرسیون متعامد می باشد و می تواند هم در مدل های خطی و هم در مدل های غیر خطی به کار برده شود. [ ۱] [ ۲]
تقریب مجموع کمترین مربعات داده ها به طور کلی معادل بهترین، در نُرم فروبنیوس، تقریب رتبه پایین ماتریس داده است.
در روش کمترین مربعات مدل سازی داده ها، تابع هدف، S ,
S = r T W r ,
به حداقل می رسد، که r بردار باقیمانده ها و W یک ماتریس وزنی است. در کمترین مربعات خطی، مدل شامل معادلاتی است که در پارامترهای ظاهر شده در بردار پارامتر خطی هستند. β، بنابراین باقیمانده ها توسط داده می شوند.
r = y − X β .
m مشاهده در پارامترهای y و n در β با m > n وجود دارد. X یک ماتریس m × n است که عناصر آن ثابت یا توابع متغیرهای مستقل، x هستند. ماتریس وزن W در حالت ایده آل، معکوس ماتریس واریانس - کوواریانس است My از مشاهدات y فرض می شود که متغیرهای مستقل بدون خطا هستند. تخمین پارامترها با قرار دادن معادلات گرادیان بر روی صفر بدست می آیند که معادلات عادی را به دست می آورند.
X T W X β = X T W y .
حال، فرض کنید هر دو x و y مشروط به خطا، با ماتریس های واریانس کوواریانس مشاهده می شوند. Mx وMy به ترتیب. در این مورد تابع هدف را می توان به صورت نوشتاری نوشت
S = r x T M x − 1 r x + r y T M y − 1 r y ,
جایی که rx و ry باقیمانده ها به ترتیب در x و y هستند. واضح است این باقیمانده ها نمی توانند مستقل از یکدیگر باشند، اما باید توسط نوعی رابطه محدود شوند. نوشتن تابع مدل به صورت f ( rx , ry , β ) محدودیت ها با معادلات شرط m بیان می شوند.
F = Δ y − ∂ f ∂ r x r x − ∂ f ∂ r y r y − X Δ β = 0 .
بنابراین، مسئله به حداقل رساندن تابع هدف تحت قیود m، با استفاده از ضریب لاگرانژ حل می شود. پس از انجام چند عملیات جبری نتیجه زیر حاصل می شود.
X T M − 1 X Δ β = X T M − 1 Δ y ,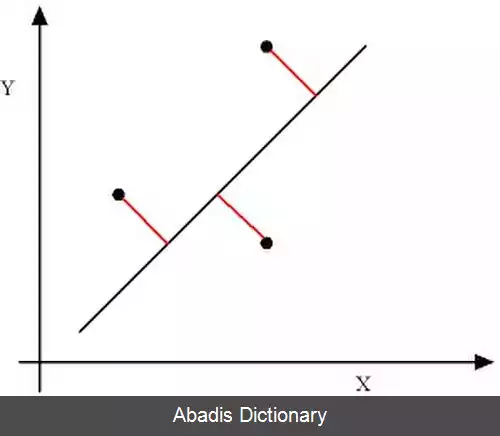
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتقریب مجموع کمترین مربعات داده ها به طور کلی معادل بهترین، در نُرم فروبنیوس، تقریب رتبه پایین ماتریس داده است.
در روش کمترین مربعات مدل سازی داده ها، تابع هدف، S ,
S = r T W r ,
به حداقل می رسد، که r بردار باقیمانده ها و W یک ماتریس وزنی است. در کمترین مربعات خطی، مدل شامل معادلاتی است که در پارامترهای ظاهر شده در بردار پارامتر خطی هستند. β، بنابراین باقیمانده ها توسط داده می شوند.
r = y − X β .
m مشاهده در پارامترهای y و n در β با m > n وجود دارد. X یک ماتریس m × n است که عناصر آن ثابت یا توابع متغیرهای مستقل، x هستند. ماتریس وزن W در حالت ایده آل، معکوس ماتریس واریانس - کوواریانس است My از مشاهدات y فرض می شود که متغیرهای مستقل بدون خطا هستند. تخمین پارامترها با قرار دادن معادلات گرادیان بر روی صفر بدست می آیند که معادلات عادی را به دست می آورند.
X T W X β = X T W y .
حال، فرض کنید هر دو x و y مشروط به خطا، با ماتریس های واریانس کوواریانس مشاهده می شوند. Mx وMy به ترتیب. در این مورد تابع هدف را می توان به صورت نوشتاری نوشت
S = r x T M x − 1 r x + r y T M y − 1 r y ,
جایی که rx و ry باقیمانده ها به ترتیب در x و y هستند. واضح است این باقیمانده ها نمی توانند مستقل از یکدیگر باشند، اما باید توسط نوعی رابطه محدود شوند. نوشتن تابع مدل به صورت f ( rx , ry , β ) محدودیت ها با معادلات شرط m بیان می شوند.
F = Δ y − ∂ f ∂ r x r x − ∂ f ∂ r y r y − X Δ β = 0 .
بنابراین، مسئله به حداقل رساندن تابع هدف تحت قیود m، با استفاده از ضریب لاگرانژ حل می شود. پس از انجام چند عملیات جبری نتیجه زیر حاصل می شود.
X T M − 1 X Δ β = X T M − 1 Δ y ,

wiki: مجموع کمترین مربعات
