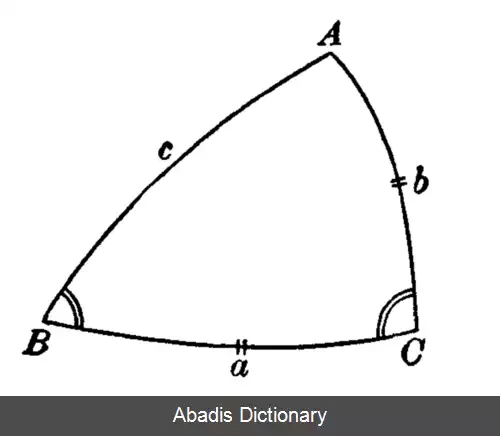
مثلثات کروی علمی است که به بررسی روابط بین زاویه ها و اضلاع یک مثلث کروی ( در هندسه نااقلیدسی ) می پردازد. مثلثات کروی شاخه ای از هندسه کروی است که با توجه به روابط بین توابع مثلثاتی دو طرف و زوایای چند ضلعی کروی ( به ویژه مثلث کروی ) ؛ محدود شده توسط تعدادی از دایره های بزرگ، در کره را بررسی می کند. کاربرد عملی مثلثات کروی در محاسبه ها و براوردها در نجوم رصدی، زمین شناسی و ناوبری، و نیز قبله یابی، بسیار مهم است.
در این مثلث ها مجموع زوایای داخلی بیشتر از ۱۸۰ درجه و حداکثر ۵۴۰ درجه می باشد. [ ۱]
قوانین معمول مثلثات تخت در این مثلثات صادق نیستند.
تمام اضلاع این مثلثات باید جزو دوایر عظیمه باشند.
( CT1 ) cos b cos C = cot a sin b − cot A sin C , ( a C b A ) ( CT2 ) cos b cos A = cot c sin b − cot C sin A , ( C b A c ) ( CT3 ) cos c cos A = cot b sin c − cot B sin A , ( b A c B ) ( CT4 ) cos c cos B = cot a sin c − cot A sin B , ( A c B a ) ( CT5 ) cos a cos B = cot c sin a − cot C sin B , ( c B a C ) ( CT6 ) cos a cos C = cot b sin a − cot B sin C , ( B a C b ) .
منابع
↑ ( Merserve، pp. 281 - 282 )
• نجوم کروی، ویلیام مارشال اسمارت
• Meserve, Bruce E. ( 1983 ) , Fundamental Concepts of Geometry, Dover, ISBN 0 - 486 - 63415 - 9
• Smart, W. M. ( 1986 ) . Text - Book on Spherical Astronomy ( 6th ed. ) . Cambridge University Press. The fourth edition is online at archive. org. Chapter 1 is on spherical trigonometry with numerical examples. {{cite book}}: External link in | postscript= ( help ) نگهداری CS1: پست اسکریپت ( link ) چاپ چهارم کتاب متنی Text - Book اسمارت در اخترشناسی کروی
• https://en. wikipedia. org/wiki/Spherical_trigonometry
• مثلثات کروی
• خطاهای یادکرد: پیوندهای بیرونی
• نگهداری CS1: پست اسکریپت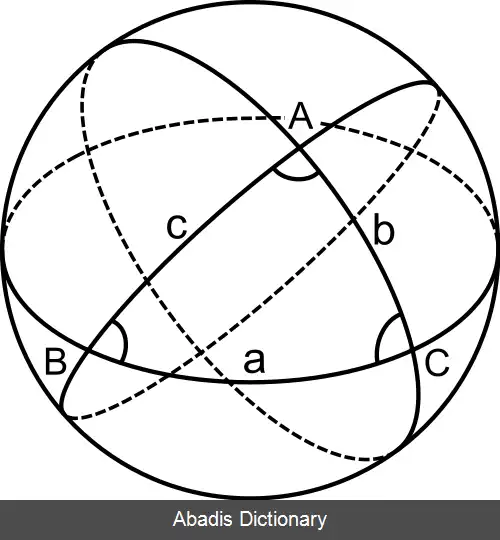
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر این مثلث ها مجموع زوایای داخلی بیشتر از ۱۸۰ درجه و حداکثر ۵۴۰ درجه می باشد. [ ۱]
قوانین معمول مثلثات تخت در این مثلثات صادق نیستند.
تمام اضلاع این مثلثات باید جزو دوایر عظیمه باشند.
( CT1 ) cos b cos C = cot a sin b − cot A sin C , ( a C b A ) ( CT2 ) cos b cos A = cot c sin b − cot C sin A , ( C b A c ) ( CT3 ) cos c cos A = cot b sin c − cot B sin A , ( b A c B ) ( CT4 ) cos c cos B = cot a sin c − cot A sin B , ( A c B a ) ( CT5 ) cos a cos B = cot c sin a − cot C sin B , ( c B a C ) ( CT6 ) cos a cos C = cot b sin a − cot B sin C , ( B a C b ) .
منابع
↑ ( Merserve، pp. 281 - 282 )
• نجوم کروی، ویلیام مارشال اسمارت
• Meserve, Bruce E. ( 1983 ) , Fundamental Concepts of Geometry, Dover, ISBN 0 - 486 - 63415 - 9
• Smart, W. M. ( 1986 ) . Text - Book on Spherical Astronomy ( 6th ed. ) . Cambridge University Press. The fourth edition is online at archive. org. Chapter 1 is on spherical trigonometry with numerical examples. {{cite book}}: External link in | postscript= ( help ) نگهداری CS1: پست اسکریپت ( link ) چاپ چهارم کتاب متنی Text - Book اسمارت در اخترشناسی کروی
• https://en. wikipedia. org/wiki/Spherical_trigonometry
• مثلثات کروی
• خطاهای یادکرد: پیوندهای بیرونی
• نگهداری CS1: پست اسکریپت


wiki: مثلثات کروی
