مثلث متساوی الساقین

دانشنامه عمومی

مثلث متساوی الساقین ( به فارسی: سه گوشه همسان پا ) مثلثی است که دو ضلع با طول برابر داشته باشد. در تعریف گسترده تر، این مثلث حداقل دو ضلع برابر دارد که به این ترتیب مثلث متساوی الاضلاع نیز حالت خاصی از مثلث متساوی الساقین به شمار می رود. مثلث متساوی الساقین برای مثال در مثلث طلایی، وجوه دوهرم و برخی اجسام کاتالان دیده می شود.
تاریخچه مطالعه ریاضی مثلث متساوی الساقین به ریاضیات مصر باستان و ریاضیات بابلیان برمی گردد. استفاده از مثلث متساوی الساقین در طراحی ساختمان نیز قدمتی طولانی دارد و برای مثال در سنتوری ساختمان های یونانی و رومی مشاهده می شود.
دو ضلع یکسان مثلث متساوی الساقین، ساق و ضلع سوم قاعدهٔ مثلث خوانده می شوند. سایر اندازه های مثلث متساوی الساقین همچون ارتفاع، مساحت و محیط آن با کمک فرمول های ساده ای از اندازه ساق و قاعدهٔ مثلث قابل محاسبه هستند. عمود منصف قاعدهٔ هر مثلث متساوی الساقین، محور تقارن آن نیز هست. دو زاویهٔ روبرو به ساق های مثلث متساوی الساقین با یکدیگر برابر و همواره حاده هستند.
۱ ) در مثلث متساوی الساقین نیمساز و میانه و ارتفاع در راس بالایی بر هم منطبق هستند
۲ ) نیمساز خارجی راس مثلث متساوی الساقین با قاعده موازی است و برابر با زاویه های پای ساق ها می باشد.
۳ ) در مثلث متساوی الساقین، اندازه زاویه ی خارجی یکی از راس های آن، با مجموع دو زاویه ی غیر مجاور برابر است.
قضیه پل خربگیری: اگر دو ساق بایکدیگر برابر باشند، زوایای پای دو ساق با یکدیگر برابرند.
عکس قضیه: اگر زوایای پای دو ساق برابر باشد، دو ساق با یکدیگر برابرند و مثلث متساوی الساقین می شود.
مشارکت کنندگان ویکی پدیا. «hossin ezy». در دانشنامهٔ ویکی پدیای انگلیسی، بازبینی شده در 10مارس 2021.
• مثلث ها
• انواع مثلث ها
• مقاله های بدون منبع از دسامبر ۲۰۱۵
• همه مقاله های بدون منبع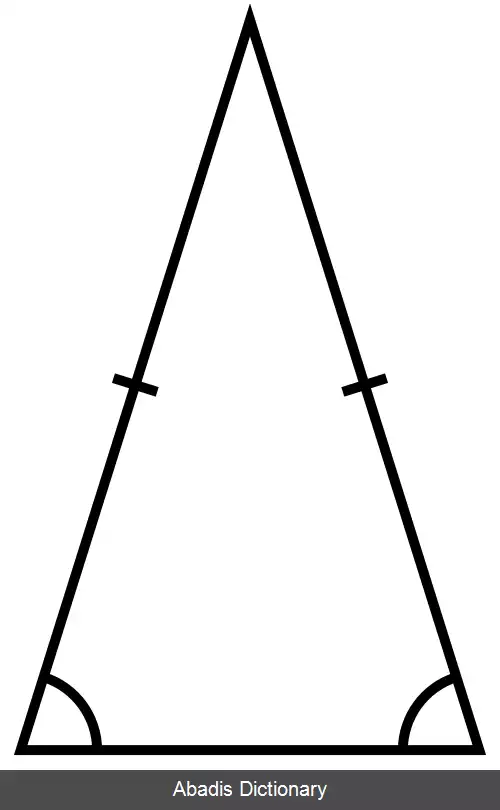
عکس مثلث متساوی الساقین
wiki: مثلث متساوی الساقین
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف

دانشنامه آزاد فارسی

مثلث مُتَساویُ السّاقَیْن (isosceles triangle)
صفت مثلثی با دو ضلعبرابر، و درنتیجه، دو زاویۀ مجاوربه قاعدۀ برابر. محور تقارناین مثلث ارتفاعآن است. همچنین، به ذوزنقه ای با دو ضلع غیرموازیِ برابر نیز ذوزنقۀ متساوی الساقینمی گویند.
wikijoo: مثلث_متساوی_الساقین

پیشنهاد کاربران

انواع مثلث به انگلیسی:
✅ right triangle / right - angled triangle = مثلث قائم الزاویه
✅ scalene triangle = مثلث مختلف الاضلاع
✅ isosceles triangle = مثلث متساوی الساقین
✅ equilateral triangle = مثلث متساوی الاضلاع
مثلث متساوی الساقین
اشکال هندسی:
circle = دایره
ellipse = بیضی
square = مربع
rectangle = مستطیل
rectangular prism / cuboid = مکعب مستطیل
triangle = مثلث
right triangle / right - angled triangle = مثلث قائم الزاویه
... [مشاهده متن کامل]

scalene triangle = مثلث مختلف الاضلاع
isosceles triangle = مثلث متساوی الساقین
equilateral triangle = مثلث متساوی الاضلاع
rhombus = لوزی
parallelogram = متوازی الاضلاع
trapezium / trapezoid = ذوزنقه
cube = مکعب
cone = مخروط
cylinder = استوانه
prism = منشور
pyramid = هرم
sphere = کُره
polygon = چند ضلعی
regular polygon = چند ضلعی منتظم
pentagon = پنج ضلعی
hexagon = شش ضلعی
heptagon = هفت ضلعی
octagon = هشت ضلعی
nonagon = نه ضلعی
decagon = ده ضلعی

سگوش همساگ
مثلث = triangle = سه گوشه ( angle : گوشه ، tri : سه )
مثلث متساوی الساقین = isosceles triangle = سه گوشه همسان پا ( iso : همسان ، scele : پا )
مثلث متساوی الاضلاع = equilateral triangle = سه گوشه همسان بَر
کوهانه ، سه گوش کوهانه ، سه گوش کوهوار ، سه گوش بلند ، سه کنج ( سکُنج ) بلند، سکنج کوهانه

بپرس