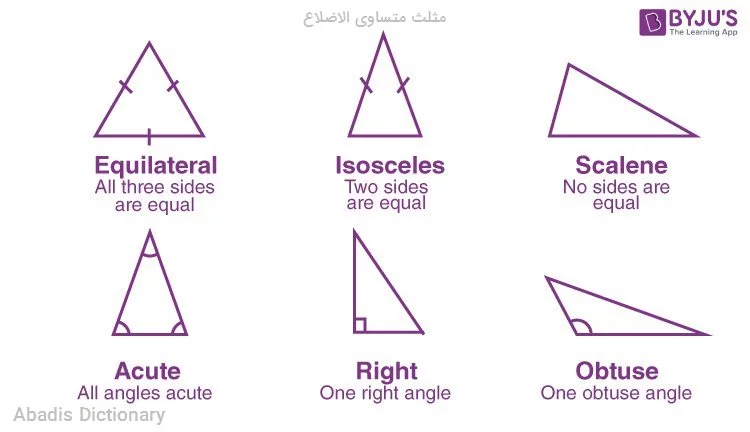
مثلث متساوی الاضلاع ( به انگلیسی: Equilateral triangle ) یا سه گوشه همسان بَر در هندسه به مثلثی گفته می شود که سه ضلع آن برابر باشند. در این مثلث هر سه زاویه داخلی نیز برابرند و اندازه هرکدام ۶۰ درجه است. زوایای خارجی این مثلث نیز برابر بوده و هرکدام ۱۲۰ درجه هستند. همچنین این مثلّث حالت خاصّی از مثلّث های متساوی الساقین است. [ ۱]
.
با فرضِ اینکه درازای اضلاع مثلث متساوی الاضلاع a باشد، خواهیم داشت:
• مساحت: a 2 3 4 {\displaystyle a^{2}{\frac {\sqrt {3}}{4}}}
• محیط: P = 3 a {\displaystyle P=3a\, \!}
• شعاع دایرهٔ محیطی: r = a 3 3 {\displaystyle r=a{\frac {\sqrt {3}}{3}}}
• شعاع دایرهٔ محاطی: r = a 3 6 {\displaystyle r=a{\frac {\sqrt {3}}{6}}}
• و ارتفاع: a 3 2 {\displaystyle a{\frac {\sqrt {3}}{2}}} .
این روابط را می توان از قضیه فیثاغورس نتیجه گرفت.
ویژگی های هندسی این مثلث به این ترتیب می باشد.
• دارای ۳ خط تقارن است
• هر سه زاویهٔ آن با هم برابرند، بنابر این دارای ۳ زاویه ۶۰ درجه است.
• دارای یک مرکز تقارن است.
رسم مثلث متساوی الاضلاع با استفاده از خط کش و پرگار به صورت پویانمایی زیر است.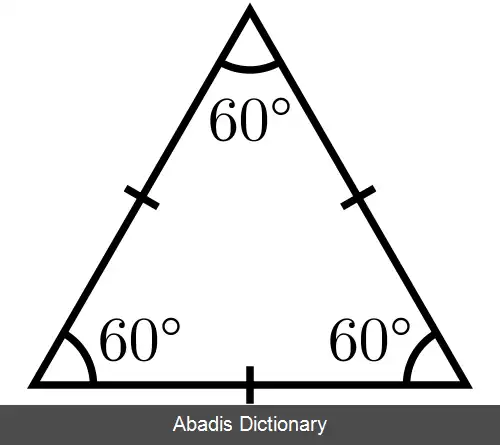

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف.
با فرضِ اینکه درازای اضلاع مثلث متساوی الاضلاع a باشد، خواهیم داشت:
• مساحت: a 2 3 4 {\displaystyle a^{2}{\frac {\sqrt {3}}{4}}}
• محیط: P = 3 a {\displaystyle P=3a\, \!}
• شعاع دایرهٔ محیطی: r = a 3 3 {\displaystyle r=a{\frac {\sqrt {3}}{3}}}
• شعاع دایرهٔ محاطی: r = a 3 6 {\displaystyle r=a{\frac {\sqrt {3}}{6}}}
• و ارتفاع: a 3 2 {\displaystyle a{\frac {\sqrt {3}}{2}}} .
این روابط را می توان از قضیه فیثاغورس نتیجه گرفت.
ویژگی های هندسی این مثلث به این ترتیب می باشد.
• دارای ۳ خط تقارن است
• هر سه زاویهٔ آن با هم برابرند، بنابر این دارای ۳ زاویه ۶۰ درجه است.
• دارای یک مرکز تقارن است.
رسم مثلث متساوی الاضلاع با استفاده از خط کش و پرگار به صورت پویانمایی زیر است.


wiki: مثلث متساوی الاضلاع