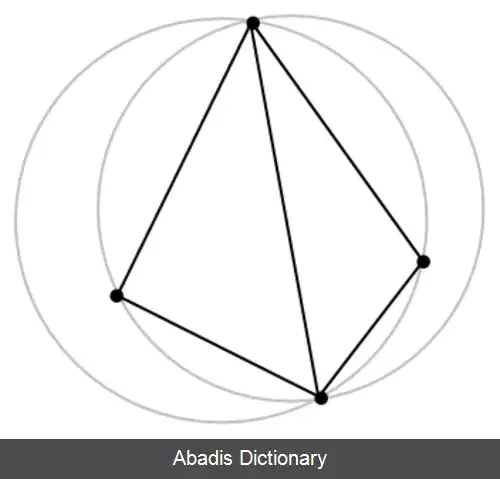
در ریاضیات و هندسهٔ محاسباتی، یک مثلث بندی دیلانی برای یک مجموعه از نقاط به نام P در یک صفحه، یک مثلث بندی به نام ( DT ( P است به نحوی که هیچ یک از نقاط P درون هیچ یک از دایره های محیطی مثلثهای ( DT ( P نباشد. این مثلث بندی کمینهٔ زاویه های مثلثها را به بیشترین مقدار ممکن می رساند و به این ترتیب از به وجود آمدن مثلث های باریک جلوگیری می کند. این مثلث بندی توسط بوریس دیلانی در سال ۱۹۳۴ ابداع شد. [ ۱] برای چهار یا تعداد بیشتری نقطه روی یک دایره یکسان ( به عنوان مثال رأس های یک مستطیل ) تثلیث دیلانی یکتا نیست : هر دو تثلیث ممکن که چهار ضلعی را به دو مثلث تقسیم می کند شرط دیلانی ارضا می کند به عنوان مثال فرض اینکه اگر تمام دایره های محیطی مثلث ها درون تهی باشند. با در نظر گرفتن کره های محاطی ایدهٔ تثلیث دیلانی به سه یا تعداد بیشتری بعد تعمیم می یابد . تعمیم به سیستم متریک نسبت به سیستم اقلیدسی ترجیح داده می شود ولی در این موارد ( اقلیدسی ) تثلیث دیلانی الزاماً وجود ندارد یا یکتا نیست.
تثلیث دیلانی در فضای گسسته مجموعه p در جنرال پوزیشن مربوط به گراف های دوگانه از دیاگرام ورونی از مجموعه p. موردهای خاصی که شامل سه نقطه ای که روی یک خط اند و چهار نقطهای که روی یک دایره اند.
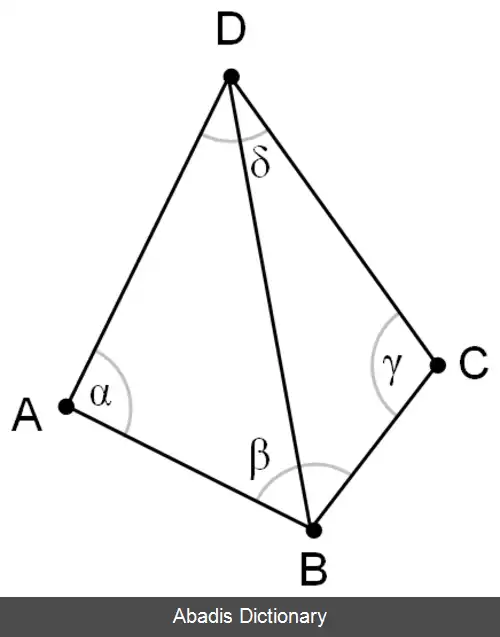
دیلانی d بعدی برای مجموع نقاط p در فضای فضای اقلیدسی اقلیدسی d بعدی تثلیث دیلانی ( DT ( p است به طوری که هیچ نقطهای در P درون ابر کره محیطی هر سیمپلکس در ( DT ( P نباشد . اثبات شده[ ۲] که در برای هر p یک تثلیث دیلانی یکتا وجود دارد که p گروهی از نقاط در جنرال پوزیشن باشند که نتیجه می دهد هیچ زیر فضای k بعدی آن شامل k + 2 نقطه یا کره k بعدی شامل k + 3 نقطه نباشد برای 1 ≤ k ≤ d − 1 ( برای مثال برا ی یک مجموعه نقاط در ℝ3 هیچ سه نقطه ای روی یک خط وجود ندارند، هیچ چهار نقطه ای روی یک صفحه، هیچ چهار نقطه ای روی یک دایره و هیچ 5 نقطه ای روی یک کره وجود ندارد ) مسئله پیدا کردن تثلیث دیلانی برای گروهی از نقاط در فضای ی بعدی اقلیدسی قابل تبدیل به مسئلهٔ یافتن پوش محدب برای یک مجموعه نقاط در فضای d + 1 بعدی با دادن مختصات اضافی p|2|، به هر نقطه p و گرفتن گوشه پایین پوش محدب و نگاشتن مجدد به فضای d بعدی با حذف مختصات اخیر است. چون پوش محدب یکتاست بنابراین تثلیث نیز یکتاست با فرض اینکه تمام اضلاع پوش محدب سیمپلکس هستند . اضلاع غیر سیمپلکس تنها زمانی پدید می آیند که d + 2 تا از نقاط اصلی روی یک ابر کرهابر کره دی بعدی باشند به عنوان مثال نقاط در جنرال پوزیشن نباشند.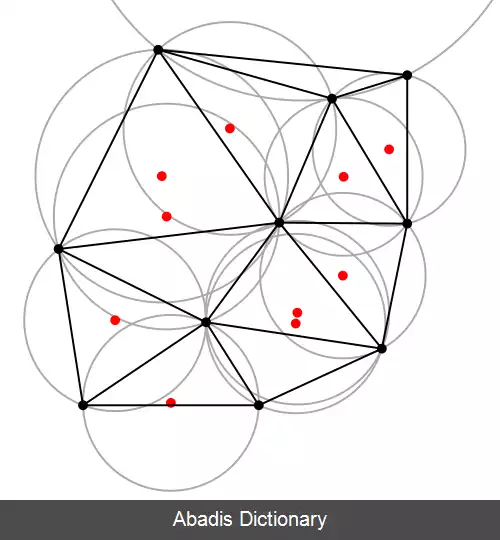
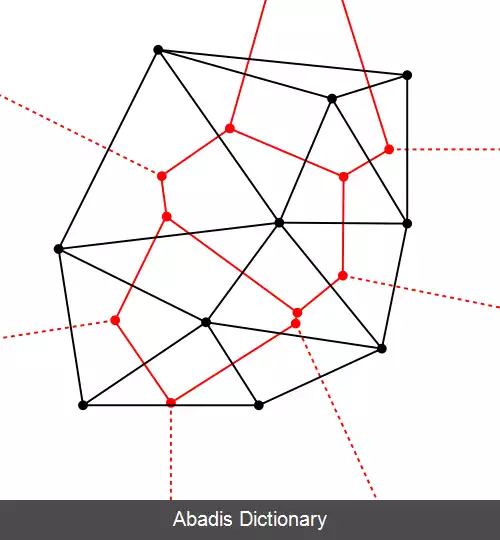
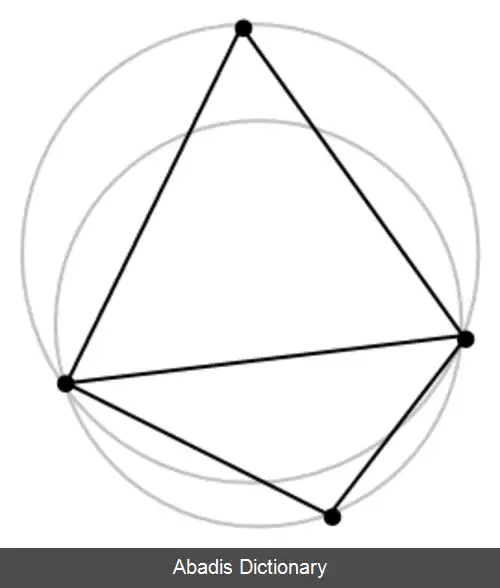
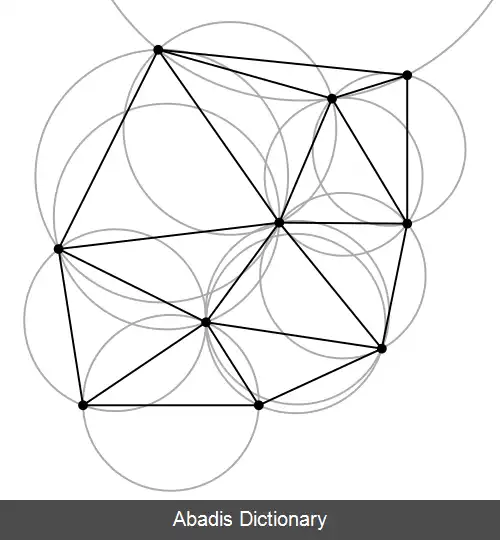
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتثلیث دیلانی در فضای گسسته مجموعه p در جنرال پوزیشن مربوط به گراف های دوگانه از دیاگرام ورونی از مجموعه p. موردهای خاصی که شامل سه نقطه ای که روی یک خط اند و چهار نقطهای که روی یک دایره اند.
دیلانی d بعدی برای مجموع نقاط p در فضای فضای اقلیدسی اقلیدسی d بعدی تثلیث دیلانی ( DT ( p است به طوری که هیچ نقطهای در P درون ابر کره محیطی هر سیمپلکس در ( DT ( P نباشد . اثبات شده[ ۲] که در برای هر p یک تثلیث دیلانی یکتا وجود دارد که p گروهی از نقاط در جنرال پوزیشن باشند که نتیجه می دهد هیچ زیر فضای k بعدی آن شامل k + 2 نقطه یا کره k بعدی شامل k + 3 نقطه نباشد برای 1 ≤ k ≤ d − 1 ( برای مثال برا ی یک مجموعه نقاط در ℝ3 هیچ سه نقطه ای روی یک خط وجود ندارند، هیچ چهار نقطه ای روی یک صفحه، هیچ چهار نقطه ای روی یک دایره و هیچ 5 نقطه ای روی یک کره وجود ندارد ) مسئله پیدا کردن تثلیث دیلانی برای گروهی از نقاط در فضای ی بعدی اقلیدسی قابل تبدیل به مسئلهٔ یافتن پوش محدب برای یک مجموعه نقاط در فضای d + 1 بعدی با دادن مختصات اضافی p|2|، به هر نقطه p و گرفتن گوشه پایین پوش محدب و نگاشتن مجدد به فضای d بعدی با حذف مختصات اخیر است. چون پوش محدب یکتاست بنابراین تثلیث نیز یکتاست با فرض اینکه تمام اضلاع پوش محدب سیمپلکس هستند . اضلاع غیر سیمپلکس تنها زمانی پدید می آیند که d + 2 تا از نقاط اصلی روی یک ابر کرهابر کره دی بعدی باشند به عنوان مثال نقاط در جنرال پوزیشن نباشند.






wiki: مثلث بندی دیلانی
