لغت نامه دهخدا
فرهنگ فارسی
فرهنگ عمید
دانشنامه عمومی
در هندسه، متوازی السطوح یک حجم هندسی است که از شش وجه تشکیل شده و هر یک از این وجه ها متوازی الاضلاع بوده و هر دو وجه مقابل متساوی و متوازی است. متوازی السطوح از انواع منشور است.
حجم هر چهار وجهی که دارای سه یال همگرای متوازی الاضلاع است، حجمی برابر با یک ششم حجم آن متوازی الاضلاع دارد.
حجم یک متوازی السطوح با ضلع های مساوی با مکعب باهم برابر اند.
• هر یک از سه جفت وجه موازی را می توان به عنوان صفحات پایه منشور مشاهده کرد. یک متوازی الاضلاع دارای سه مجموعه از چهار یال موازی است. لبه های هر مجموعه دارای طول مساوی هستند.
• متوازی الاضلاع از تبدیل های خطی یک مکعب ( برای موارد غیر انحطاط: تبدیل خطی دوطرفه ) حاصل می شود.
• از آنجایی که هر وجه دارای تقارن نقطه ای است , متوازی الاضلاع یک زونهدرون است . همچنین کل متوازی الاضلاع دارای تقارن نقطه ای C i است ( همچنین به triclinic مراجعه کنید ) . هر صورت، از بیرون، تصویر آینه ای از چهره مقابل است. صورت ها به طور کلی کایرال هستند ، اما موازی شکل نیست.
• با رونوشت های همخوان از هر موازی پایه ای امکان پذیر است که فضا را پر کند.
• اگر همه ضلع های مکعب را به یک زاویه برابر مورب کنیم به یک متوازی السطوح تبدیل می شود که تمام وجه هایش لوزی است و مساحت وجه های متوازی السطوح با با مساحت وجه های مکعب برابر است.
• متوازی السطوح از انواع منشورها است
• متوازی السطوح را می توان یکی از چندوجهی ها گفت
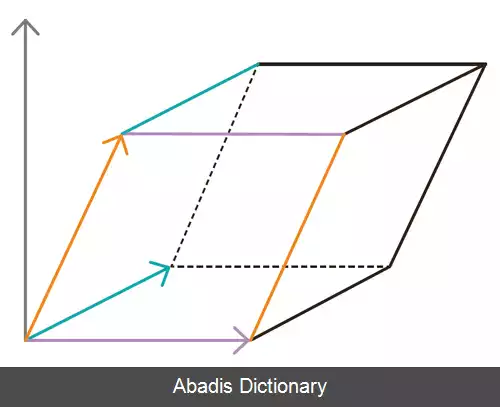
متوازی السطوح حجمی است که از سه بردار سه بعدی a, b, cدرست شده است و با ضرب خارجی بردار ها درست شده است.
ابتدا متوازی السطوحی رسم می کنیم که در فضای برداری باشد و در فضای سه بعدیR3قرار می دهیم. بردار های آن اینگونه است که:
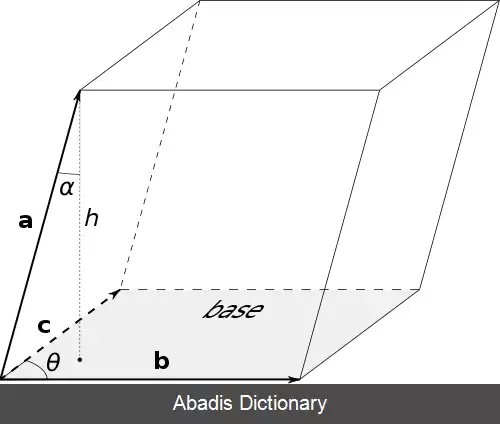
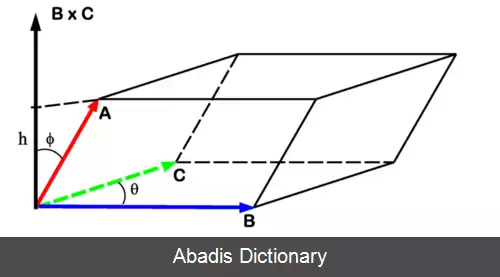
• S = | a | ⋅ | b | ⋅ sin γ = | a × b | {\displaystyle S=\left|\mathbf {a} \right|\cdot \left|\mathbf {b} \right|\cdot \sin \gamma =\left|\mathbf {a} \times \mathbf {b} \right|}
• h = | c | ⋅ | cos θ | {\displaystyle h=\left|\mathbf {c} \right|\cdot \left|\cos \theta \right|}
محاسبه حجم اینگونه است مساحت قاعده بر اساس مساحت متوازی الاضلاع بدست آید و ارتفاع آن بر اساس رابطه فیثاغورس بدست آید. پس حجم متوازی السطوح برابر با این رابطه است.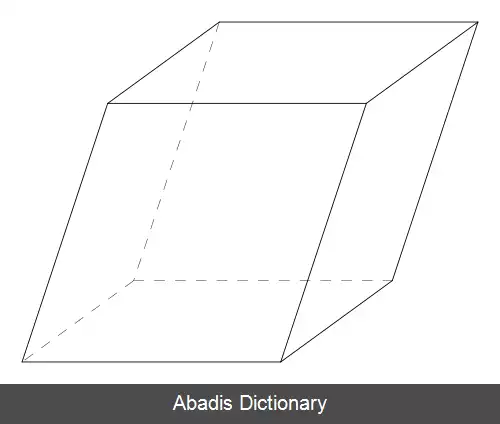
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفحجم هر چهار وجهی که دارای سه یال همگرای متوازی الاضلاع است، حجمی برابر با یک ششم حجم آن متوازی الاضلاع دارد.
حجم یک متوازی السطوح با ضلع های مساوی با مکعب باهم برابر اند.
• هر یک از سه جفت وجه موازی را می توان به عنوان صفحات پایه منشور مشاهده کرد. یک متوازی الاضلاع دارای سه مجموعه از چهار یال موازی است. لبه های هر مجموعه دارای طول مساوی هستند.
• متوازی الاضلاع از تبدیل های خطی یک مکعب ( برای موارد غیر انحطاط: تبدیل خطی دوطرفه ) حاصل می شود.
• از آنجایی که هر وجه دارای تقارن نقطه ای است , متوازی الاضلاع یک زونهدرون است . همچنین کل متوازی الاضلاع دارای تقارن نقطه ای C i است ( همچنین به triclinic مراجعه کنید ) . هر صورت، از بیرون، تصویر آینه ای از چهره مقابل است. صورت ها به طور کلی کایرال هستند ، اما موازی شکل نیست.
• با رونوشت های همخوان از هر موازی پایه ای امکان پذیر است که فضا را پر کند.
• اگر همه ضلع های مکعب را به یک زاویه برابر مورب کنیم به یک متوازی السطوح تبدیل می شود که تمام وجه هایش لوزی است و مساحت وجه های متوازی السطوح با با مساحت وجه های مکعب برابر است.
• متوازی السطوح از انواع منشورها است
• متوازی السطوح را می توان یکی از چندوجهی ها گفت
متوازی السطوح حجمی است که از سه بردار سه بعدی a, b, cدرست شده است و با ضرب خارجی بردار ها درست شده است.
ابتدا متوازی السطوحی رسم می کنیم که در فضای برداری باشد و در فضای سه بعدیR3قرار می دهیم. بردار های آن اینگونه است که:
• S = | a | ⋅ | b | ⋅ sin γ = | a × b | {\displaystyle S=\left|\mathbf {a} \right|\cdot \left|\mathbf {b} \right|\cdot \sin \gamma =\left|\mathbf {a} \times \mathbf {b} \right|}
• h = | c | ⋅ | cos θ | {\displaystyle h=\left|\mathbf {c} \right|\cdot \left|\cos \theta \right|}
محاسبه حجم اینگونه است مساحت قاعده بر اساس مساحت متوازی الاضلاع بدست آید و ارتفاع آن بر اساس رابطه فیثاغورس بدست آید. پس حجم متوازی السطوح برابر با این رابطه است.




wiki: متوازی السطوح
دانشنامه آزاد فارسی
مُتَوازیُ السُطوح (parallelepiped)
منشوری با قاعده های متوازی الاضلاع. به عبارت دیگر، چندوجهیای که همۀ وجوه آن متوازی الاضلاع باشند.
منشوری با قاعده های متوازی الاضلاع. به عبارت دیگر، چندوجهیای که همۀ وجوه آن متوازی الاضلاع باشند.
wikijoo: متوازی_السطوح
مترادف ها
متوازی السطوح، حجم متوازی السطوح، منشور متوازی السطوح
پیشنهاد کاربران
همراستا رویه
