در آمار و به طور خاص در برازش مدل های رگرسیون خطی یا رگرسیون لجستیک، شبکه الاستیک ( به انگلیسی: elastic net ) یک روش برای تنظیم ( متعادل سازی ) است که به طور خطی جریمه های نرم یک ( L1 - norm ) و نرم دو ( L2 - norm ) که به صورت جداگانه در روش های لسو و تنظیم تیخونوف استفاده می شوند را ترکیب می کند و به نوعی کاستی های این دو روش را پوشش می دهد.
به طور کلی در پیاده سازی الگوریتم های یادگیری ماشین و به طور خاص الگوریتم های مبتنی بر رگرسیون این امکان وجود دارد که مقادیر وزن ها و ایرپارامترهای مدل از کنترل خارج شوند به شکلی که یا خیلی بزرگ یا خیلی کوچک شوند یا به نوعی تمرین داده شوند که به مقادیر مجموعه تمرین بیش برازش کنند و در نتیجه عملکرد ضعیفی روی داده های تست نشان دهند. در این شرایط است که عموماً از روش های تعدیل سازی و عمومی سازی استفاده می شود تا از مشکلات گفته شده جلوگیری شود.
روش LASSO براساس نرم یک، ‖ ω ‖ 1 = ∑ j = 1 p | ω j | کار می کند و جریمه ای به همین شکل را به عبارتی که کمینه می کند، می افزاید. اینکار باعث می شود که مقادیر ω به صفر نزدیک شوند و مقادیری بزرگ به خود نگیرند ( به اصطلاح خلوت ) و به این شکل از بیش برازش جلوگیری شود. در مسئله رگرسیون تابع خطا با استفاده از تنظیم LASSO، به شکل زیر تغییر می کند:
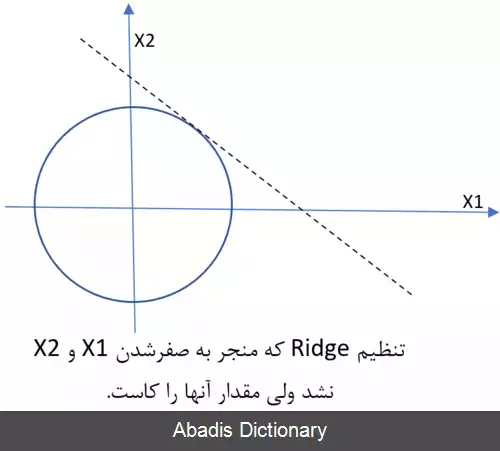
1 2 m Σ i = 1 m ( y − X w ) 2 + α Σ j = 1 p ∣ w j ∣ که عبارت اول همان خطای کمترین مربعات و عبارت دوم ترم تعدیل ساز LASSO است. لازم است ذکر شود که α ضریب تعدیل ساز نامیده می شود و با تغییر آن می توان مشخص کرد که تأثیر عبارت تعدیل ساز در تابع جریمه چقدر باشد. استفاده از این تابع جریمه محدودیت هایی دارد[ ۱] به عنوان مثال، در مواردی که تعداد داده ها از تعداد ویژگی ها بیشتر است استفاده از این روش موجب به صفر شدن بسیاری از ویژگی ها می شود. . همچنین اگر گروهی از متغیرهای بسیار همبسته وجود داشته باشد، LASSO تمایل دارد یک متغیر را از یک گروه انتخاب کند و بقیه را نادیده بگیرد. تنظیم تیخونوف مقالهٔ اصلی: تنظیم تیخونوف شهود تنظیم Ridge ( نرم ۲ ) در روش RIDGE از نرم دو ‖ ω ‖ 2 = ∑ j = 1 p ω j 2 برای تعدیل سازی استفاده می شود، پس در مورد تابع خطای رگرسیون داریم: Σ i = 1 m ( y − X w ) 2 + α Σ j = 1 p w j 2 در این روش برخلاف روش LASSO، وزن ها تمایل دارند به جای صفر شدن با هم کوچک شوند. تعدیل ساز کشسان برای غلبه بر محدودیت های دو روش قبلی، تعدیل ساز کشسان هردو عبارت را در تابع خطا استفاده می کند و رابطه زیر حاصل می شود: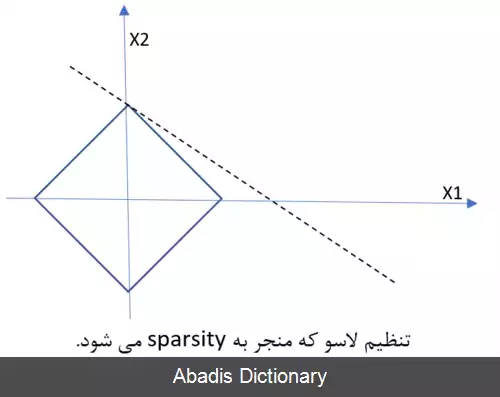
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبه طور کلی در پیاده سازی الگوریتم های یادگیری ماشین و به طور خاص الگوریتم های مبتنی بر رگرسیون این امکان وجود دارد که مقادیر وزن ها و ایرپارامترهای مدل از کنترل خارج شوند به شکلی که یا خیلی بزرگ یا خیلی کوچک شوند یا به نوعی تمرین داده شوند که به مقادیر مجموعه تمرین بیش برازش کنند و در نتیجه عملکرد ضعیفی روی داده های تست نشان دهند. در این شرایط است که عموماً از روش های تعدیل سازی و عمومی سازی استفاده می شود تا از مشکلات گفته شده جلوگیری شود.
روش LASSO براساس نرم یک، ‖ ω ‖ 1 = ∑ j = 1 p | ω j | کار می کند و جریمه ای به همین شکل را به عبارتی که کمینه می کند، می افزاید. اینکار باعث می شود که مقادیر ω به صفر نزدیک شوند و مقادیری بزرگ به خود نگیرند ( به اصطلاح خلوت ) و به این شکل از بیش برازش جلوگیری شود. در مسئله رگرسیون تابع خطا با استفاده از تنظیم LASSO، به شکل زیر تغییر می کند:
1 2 m Σ i = 1 m ( y − X w ) 2 + α Σ j = 1 p ∣ w j ∣ که عبارت اول همان خطای کمترین مربعات و عبارت دوم ترم تعدیل ساز LASSO است. لازم است ذکر شود که α ضریب تعدیل ساز نامیده می شود و با تغییر آن می توان مشخص کرد که تأثیر عبارت تعدیل ساز در تابع جریمه چقدر باشد. استفاده از این تابع جریمه محدودیت هایی دارد[ ۱] به عنوان مثال، در مواردی که تعداد داده ها از تعداد ویژگی ها بیشتر است استفاده از این روش موجب به صفر شدن بسیاری از ویژگی ها می شود. . همچنین اگر گروهی از متغیرهای بسیار همبسته وجود داشته باشد، LASSO تمایل دارد یک متغیر را از یک گروه انتخاب کند و بقیه را نادیده بگیرد. تنظیم تیخونوف مقالهٔ اصلی: تنظیم تیخونوف شهود تنظیم Ridge ( نرم ۲ ) در روش RIDGE از نرم دو ‖ ω ‖ 2 = ∑ j = 1 p ω j 2 برای تعدیل سازی استفاده می شود، پس در مورد تابع خطای رگرسیون داریم: Σ i = 1 m ( y − X w ) 2 + α Σ j = 1 p w j 2 در این روش برخلاف روش LASSO، وزن ها تمایل دارند به جای صفر شدن با هم کوچک شوند. تعدیل ساز کشسان برای غلبه بر محدودیت های دو روش قبلی، تعدیل ساز کشسان هردو عبارت را در تابع خطا استفاده می کند و رابطه زیر حاصل می شود:


wiki: متعادل سازی کشسان
