در نظریه ماشین ها ، ماشین محدود نامتناهی ( UFA ) یک نوع به خصوص از ماشین غیرقطعی محدود ( NFA ) میباشد. هر ماشین محدود قطعی ( DFA ) یک UFA هست اما برعکسش صادق نیست. DFA و UFA و NFA دقیقاً همان کلاس زبان رسمی را میشناسد. از یک طرف یک NFA میتواند به طور نمادین کوچکتر از یک DFA معادل باشد. از یک طرف بعضی از مشکلات میتواند روی DFA ها به راحتی حل شود و روی UFA ها نه.
برای مثال یک ماشین داده شده A را در نظر بگیرید ، یک ماشین A که میتواند مکمل A را بپذیرد میتواند در زمان خطی محاسبه شود که A یک DFA هست ، معلوم نیست که آیا میتوان آن را در زمان چندجمله ای برای UFA انجام داد. از این رو UFA ها ترکیبی از دنیاهای DFA و NFA هاست . در بعضی موارد آنها منجر به ماشین کوچکتر از DFA و الگوریتم های سریع تر از NFA میشوند.
یک NFA به طور رسمی با ۵ - تاپل نشان داده میشود ، ( A= ( Q, Σ, Δ, q0, F . برای هر کلمه w = a1a2 … an یک UFA چنین است که یک NFA میباشد . در بیشتر موارد یک دنباله ای از حالات r0, r1, …, rn در Q با شرایط زیر وجود دارد :
1. r0 = q0
2. ri+1 ∈ Δ ( ri, ai+1 ) , for i = 0, …, n−1
3. rn ∈ F.
به حروف آن شرایط این را بیان می کند که اگر w توسط A پذیرفته شود دقیقاً یک مسیر پذیرش وجود خواهد داشت که آن مسیری از حالت اولیه به حالت پایانی میباشد که توسط w برچسب زده شده است.
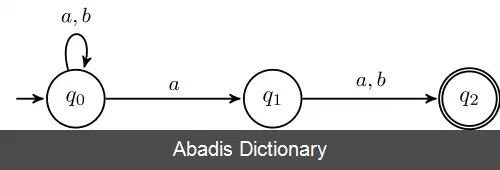
اگر L را مجموعه ای از کلمات حروف {a, b} در نظر بگیریم که nامین حرف آخرشان a میباشد . ارقام یک DFA و یک UFA را نشان میدهد که این زبان را برای n=2 میپذیرد . DFA کمینه که L را میپذیرد 2n حالت دارد که یکی از آن زیر مجموعه ها {1…n} میباشد . یک UFA با n+1 حالت وجود دارد که L را میپذیرد : که nامین حرف آخر را حدس میزند و سپس تأیید میکند که فقط n - 1 حرف مانده است . این در واقع یکنواخت است که فقط یک nامین حرف آخر وجود دارد.
۳ مشکل سخت PSPACE برای NFA های عمومی که متعلق به PTIME برای DFA هست در نظر گرفته شده است.
در زمان چندجملهای قابل حل است یا اینکه یک زبان خودکار یک زیرمجموعه از یک زبان دیگر است.
طرح اثبات پذیرش
اگر A و B دو ماشین باشند. ( L ( A و ( L ( B زبان هایی باشند که توسط این ماشین ها پذیرفته شده باشند. سپس ( L ( A ) ⊆L ( B اگر و فقط اگر ( L ( A∩ B ) =L ( A و جایی که A∩B ضرب دکارتی ماشین ها را نشان دهد ، که میتواند یکنواخت بودن را نیز ثابت کند . حال اگر ( L ( A∩B زیرمجموعه ای از ( L ( A با ساختن باشد ; بنابراین هر دو مجموعه مساوی است اگر و فقط اگر برای هر مقدار n∈ℕ تعداد طول کلمات n در ( L ( A∩B مساوی باشد با طول کلمات n در ( L ( A . میتوان ثابت کرد که کافیست تا هر n تا شماره حالات A و B چک شود .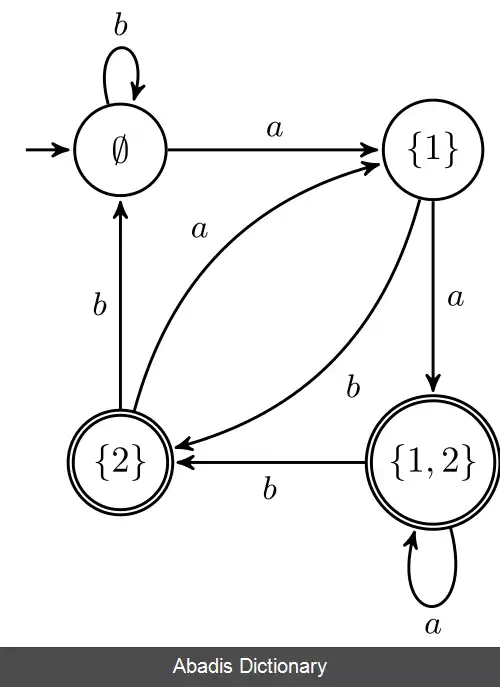
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبرای مثال یک ماشین داده شده A را در نظر بگیرید ، یک ماشین A که میتواند مکمل A را بپذیرد میتواند در زمان خطی محاسبه شود که A یک DFA هست ، معلوم نیست که آیا میتوان آن را در زمان چندجمله ای برای UFA انجام داد. از این رو UFA ها ترکیبی از دنیاهای DFA و NFA هاست . در بعضی موارد آنها منجر به ماشین کوچکتر از DFA و الگوریتم های سریع تر از NFA میشوند.
یک NFA به طور رسمی با ۵ - تاپل نشان داده میشود ، ( A= ( Q, Σ, Δ, q0, F . برای هر کلمه w = a1a2 … an یک UFA چنین است که یک NFA میباشد . در بیشتر موارد یک دنباله ای از حالات r0, r1, …, rn در Q با شرایط زیر وجود دارد :
1. r0 = q0
2. ri+1 ∈ Δ ( ri, ai+1 ) , for i = 0, …, n−1
3. rn ∈ F.
به حروف آن شرایط این را بیان می کند که اگر w توسط A پذیرفته شود دقیقاً یک مسیر پذیرش وجود خواهد داشت که آن مسیری از حالت اولیه به حالت پایانی میباشد که توسط w برچسب زده شده است.
اگر L را مجموعه ای از کلمات حروف {a, b} در نظر بگیریم که nامین حرف آخرشان a میباشد . ارقام یک DFA و یک UFA را نشان میدهد که این زبان را برای n=2 میپذیرد . DFA کمینه که L را میپذیرد 2n حالت دارد که یکی از آن زیر مجموعه ها {1…n} میباشد . یک UFA با n+1 حالت وجود دارد که L را میپذیرد : که nامین حرف آخر را حدس میزند و سپس تأیید میکند که فقط n - 1 حرف مانده است . این در واقع یکنواخت است که فقط یک nامین حرف آخر وجود دارد.
۳ مشکل سخت PSPACE برای NFA های عمومی که متعلق به PTIME برای DFA هست در نظر گرفته شده است.
در زمان چندجملهای قابل حل است یا اینکه یک زبان خودکار یک زیرمجموعه از یک زبان دیگر است.
طرح اثبات پذیرش
اگر A و B دو ماشین باشند. ( L ( A و ( L ( B زبان هایی باشند که توسط این ماشین ها پذیرفته شده باشند. سپس ( L ( A ) ⊆L ( B اگر و فقط اگر ( L ( A∩ B ) =L ( A و جایی که A∩B ضرب دکارتی ماشین ها را نشان دهد ، که میتواند یکنواخت بودن را نیز ثابت کند . حال اگر ( L ( A∩B زیرمجموعه ای از ( L ( A با ساختن باشد ; بنابراین هر دو مجموعه مساوی است اگر و فقط اگر برای هر مقدار n∈ℕ تعداد طول کلمات n در ( L ( A∩B مساوی باشد با طول کلمات n در ( L ( A . میتوان ثابت کرد که کافیست تا هر n تا شماره حالات A و B چک شود .


wiki: ماشین محدود غیرمبهم
