اسپیرال لگاریتمی ( به انگلیسی: logarithmic spiral ) یا مارپیچ لگاریتمی یا اسپیرال متساوی الزاویه یا اسپیرال رشدیابنده یک خم مارپیچ ماننده خودهمانند است که معمولاً در طبیعت دیده می شود.
اسپیرال لگاریتمی نخستین بار توسط رنه دکارت توصیف شد و بعدها توسط یاکوب برنولی به صورت گسترده مورد پژوهش قرار گرفت که وی آنها را مارپیچ لاله عباسی Spira mirabilis، "the marvelous spiral" نامید.
اسپیرال لگاریتمی هیچ حدی ندارد و شکل ثابتی است. روی هر نقطه از اسپیرال می توان به هر یک از دو سو تا بی نهایت حرکت کرد. از یک سو هرگز به مرکز نمی رسیم و از سوی خارجی نیز هرگز به انتها نمی رسیم. هسته اسپیرال لگاریتمی وقتی با میکروسکوپ مشاهده می شود همان منظره ای را دارد که وقتی به اندازه هزاران سال نوری به جلو می رویم، دارد. [ ۱]
در دستگاه مختصات قطبی ( r , θ ) منحنی لگاریتم را می توان نوشت [ ۲]
یا
با عدد e که مبنای طبیعی لگاریتم است و a و b همیشه به صورت مثبت مطلق است.
در حالت پارامتریک منحنی به شرح زیر است
با عدد حقیقی a و b .
خصوصیات اسپیرال این است که φ میان
مماس و radial line در نقطه ( r , θ ) ممتد است خصوصیات را می توان در اشکال مختلف هندسی بیان کرد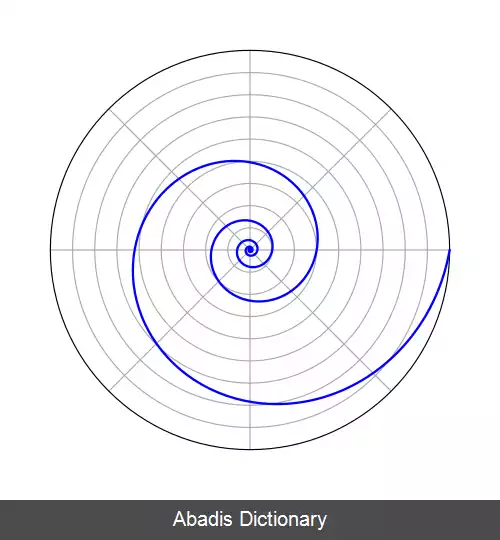





این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاسپیرال لگاریتمی نخستین بار توسط رنه دکارت توصیف شد و بعدها توسط یاکوب برنولی به صورت گسترده مورد پژوهش قرار گرفت که وی آنها را مارپیچ لاله عباسی Spira mirabilis، "the marvelous spiral" نامید.
اسپیرال لگاریتمی هیچ حدی ندارد و شکل ثابتی است. روی هر نقطه از اسپیرال می توان به هر یک از دو سو تا بی نهایت حرکت کرد. از یک سو هرگز به مرکز نمی رسیم و از سوی خارجی نیز هرگز به انتها نمی رسیم. هسته اسپیرال لگاریتمی وقتی با میکروسکوپ مشاهده می شود همان منظره ای را دارد که وقتی به اندازه هزاران سال نوری به جلو می رویم، دارد. [ ۱]
در دستگاه مختصات قطبی ( r , θ ) منحنی لگاریتم را می توان نوشت [ ۲]
یا
با عدد e که مبنای طبیعی لگاریتم است و a و b همیشه به صورت مثبت مطلق است.
در حالت پارامتریک منحنی به شرح زیر است
با عدد حقیقی a و b .
خصوصیات اسپیرال این است که φ میان
مماس و radial line در نقطه ( r , θ ) ممتد است خصوصیات را می توان در اشکال مختلف هندسی بیان کرد






wiki: مارپیچ لگاریتمی
