ماتریس متقارن
فرهنگستان زبان و ادب
دانشنامه عمومی
در جبر خطی ماتریس متقارن ( به انگلیسی: Symmetric matrix ) به ماتریسی می گویند که خودش با ترانهاده اش یکسان باشد به عبارت دیگر ماتریس A متقارن است اگر و فقط اگر:
درایه های ماتریس متقارن نسبت به قطر اصلی آن متقارن اند یعنی اگرA = ( aij ) ، بنابراین
به طور مثال ماتریس ۳×۳ زیر متقارن است
تمام ماتریس های قطری متقارن اند. تمام ماتریس های پادمتقارن درایه های قطر اصلی شان صفر است.
در مکانیک کوانتم و نظریه میدان کوانتمی برای برخوردها ماتریس متقارن مختلط نگاشته می شود که این مقاله برای ماتریس متقارن در اعداد حقیقی به کار می رود اما هر ماتریس متقارن مختلط A را می توان به صورت A = U D UT نگاشت، که U ماتریس واحد و D ماتریس قطری با درایه های نامنفی است. یکی از معمولترین کاربردهای آن این است که نشان می دهد فرمیون ها همواره جرم نامنفی و حقیقی دارند که در نقض سی پی کاربرد دارد.
هر ماتریس مربعی را می توان به صورت جمع دو ماتریس متقارن و پادمتقارن نوشت:
که ½ ( X + XT ) ∈ Symn و ½ ( X − XT ) ∈ Skewn. برای تمام ماتریس های مربعی صدق می کند.
یک ماتریس مربعی را زمانی تقارن پذیر گوییم هرگاه ماتریس قطری D و ماتریس متقارن S وجود داشته باشند که A = DS. ترانهاده یک ماتریس تقارن پذیر نیز تقارن پذیر است برای ( DS ) T = D− T ( DTSD ) . ماتریس A = ( aij ) فقط زمانی تقارن پذیر است که در شرایط زیر صدق کند:
• a i j = 0 implies a j i = 0 for all 1 ≤ i ≤ j ≤ n . {\displaystyle a_{ij}=0{\text{ implies }}a_{ji}=0{\text{ for all }}1\leq i\leq j\leq n. }
• a i 1 i 2 a i 2 i 3 … a i k i 1 = a i 2 i 1 a i 3 i 2 … a i 1 i k for any finite sequence ( i 1 , i 2 , … , i k ) . {\displaystyle a_{i_{1}i_{2}}a_{i_{2}i_{3}}\dots a_{i_{k}i_{1}}=a_{i_{2}i_{1}}a_{i_{3}i_{2}}\dots a_{i_{1}i_{k}}{\text{ for any finite sequence }} ( i_{1}, i_{2}, \dots , i_{k} ) . }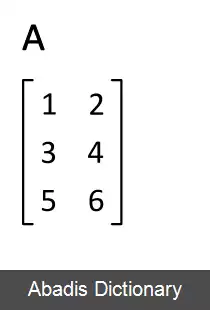
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدرایه های ماتریس متقارن نسبت به قطر اصلی آن متقارن اند یعنی اگرA = ( aij ) ، بنابراین
به طور مثال ماتریس ۳×۳ زیر متقارن است
تمام ماتریس های قطری متقارن اند. تمام ماتریس های پادمتقارن درایه های قطر اصلی شان صفر است.
در مکانیک کوانتم و نظریه میدان کوانتمی برای برخوردها ماتریس متقارن مختلط نگاشته می شود که این مقاله برای ماتریس متقارن در اعداد حقیقی به کار می رود اما هر ماتریس متقارن مختلط A را می توان به صورت A = U D UT نگاشت، که U ماتریس واحد و D ماتریس قطری با درایه های نامنفی است. یکی از معمولترین کاربردهای آن این است که نشان می دهد فرمیون ها همواره جرم نامنفی و حقیقی دارند که در نقض سی پی کاربرد دارد.
هر ماتریس مربعی را می توان به صورت جمع دو ماتریس متقارن و پادمتقارن نوشت:
که ½ ( X + XT ) ∈ Symn و ½ ( X − XT ) ∈ Skewn. برای تمام ماتریس های مربعی صدق می کند.
یک ماتریس مربعی را زمانی تقارن پذیر گوییم هرگاه ماتریس قطری D و ماتریس متقارن S وجود داشته باشند که A = DS. ترانهاده یک ماتریس تقارن پذیر نیز تقارن پذیر است برای ( DS ) T = D− T ( DTSD ) . ماتریس A = ( aij ) فقط زمانی تقارن پذیر است که در شرایط زیر صدق کند:
• a i j = 0 implies a j i = 0 for all 1 ≤ i ≤ j ≤ n . {\displaystyle a_{ij}=0{\text{ implies }}a_{ji}=0{\text{ for all }}1\leq i\leq j\leq n. }
• a i 1 i 2 a i 2 i 3 … a i k i 1 = a i 2 i 1 a i 3 i 2 … a i 1 i k for any finite sequence ( i 1 , i 2 , … , i k ) . {\displaystyle a_{i_{1}i_{2}}a_{i_{2}i_{3}}\dots a_{i_{k}i_{1}}=a_{i_{2}i_{1}}a_{i_{3}i_{2}}\dots a_{i_{1}i_{k}}{\text{ for any finite sequence }} ( i_{1}, i_{2}, \dots , i_{k} ) . }

wiki: ماتریس متقارن
پیشنهاد کاربران
پیشنهادی ثبت نشده است. شما اولین نفر باشید
