در جبر خطی, یک ماتریس متعامد ( به انگلیسی: orthogonal matrix ) , ماتریس مربعی است که درایه های آن اعداد حقیقی بوده و سطرها و ستون ها بردارهای یکه متعامد باشند.
به شکل معادل, یک ماتریس Q متعامد است اگر ترانهاده و وارون آن برابر باشد:
یا به عبارت دیگر
که I ماتریس همانی است.
یک ماتریس متعامد لزوما هم مربعی است و هم وارون پذیر
به عنوان یک تبدیل خطی یک ماتریس متعامد مقدار ضرب داخلی ( زاویه و طول بردار ) را حفظ کرده و یک تبدیل ایزومتری در فضای اقلیدسی است که شامل چرخش و بازتاب نیز هستند.
مجموعه n × n ماتریس های متعامد یک گروه O ( n ) , تشکیل می دهند که به گروه متعامد معروفند زیرگروه SO ( n ) شامل ماتریس های متعامدی است که دترمینان آنها برابر +۱ باشد و به گروه متعامد ویژه معروفند, که هر ماتریس متعماد ویژه معرف یک دوران است.
مدل مختلط ماتریس متعامد ماتریس یکانی است.
یک ماتریس متعامد ماتریسی خاص از ماتریس واحد است و بنابرین همیشه یک ماتریس نرمال خواهد بود, [ ۱] ماتریس های متعامد کاربردهای نظری و عملی بسیار زیادی دارند. یک ماتریس متعامد n×n یک گروه متعامد ( از گروه های لی ) است که با نماد O ( n ) شناخته می شود و کاربرد زیادی در بخش های مختلف علوم فیزیک و ریاضیات دارد.
بعضی از ماتریس های متعامد به شرح زیرند:
• تبدیل همانی: {\displaystyle {\begin{bmatrix}1& 0\\0& 1\\\end{bmatrix}}}
• دوران به اندازه ۱۶. ۲۶ درجه: {\displaystyle {\begin{bmatrix}0. 96& - 0. 28\\0. 28& \; \; \, 0. 96\\\end{bmatrix}}}
• بازتاب تحت محور xها: {\displaystyle {\begin{bmatrix}1& 0\\0& - 1\\\end{bmatrix}}}
ابتدایی ترین نوع ماتریس های 1×1 ماتریس و هستند.
ماتریس های 2×2 به شکل زیر هستند
به شرط برقراری سه رابطه متعامد هستند:
برای ساختن معادله اول و بدون کاستن از کلیت مسئله می توان فرض کرد p = cos θ و q = sin θ; بنابرین t = − q, u = p or t = q, u = − p. ما می توانیم اولین مورد را به عنوان دوران به اندازه زاویه θ ( که اگرθ = 0 به تبدیل همانی تبدیل می شود ) , و دومین را به عنوان بازتاب تحت خطی به زاویه θ/2.
حالت خاص بازتاب در مورد θ=90° منجر می شود به بازتاب حول خطی که در زاویه ۴۵ درجه است که به خط y=x معروف استیا به عبارت دیگر جای x و y را عوض می کند و به ماتریس تبدیل زیر نیز معروف است: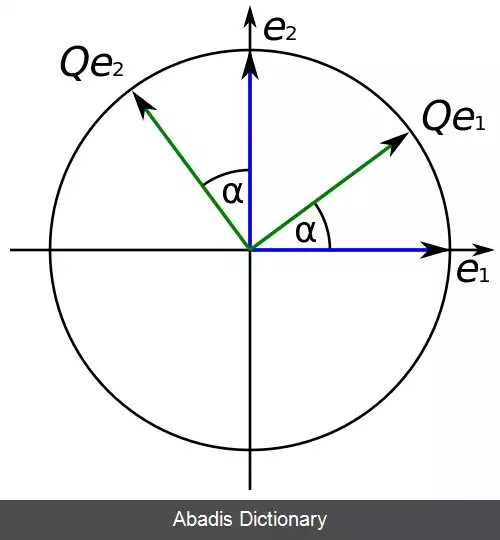
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبه شکل معادل, یک ماتریس Q متعامد است اگر ترانهاده و وارون آن برابر باشد:
یا به عبارت دیگر
که I ماتریس همانی است.
یک ماتریس متعامد لزوما هم مربعی است و هم وارون پذیر
به عنوان یک تبدیل خطی یک ماتریس متعامد مقدار ضرب داخلی ( زاویه و طول بردار ) را حفظ کرده و یک تبدیل ایزومتری در فضای اقلیدسی است که شامل چرخش و بازتاب نیز هستند.
مجموعه n × n ماتریس های متعامد یک گروه O ( n ) , تشکیل می دهند که به گروه متعامد معروفند زیرگروه SO ( n ) شامل ماتریس های متعامدی است که دترمینان آنها برابر +۱ باشد و به گروه متعامد ویژه معروفند, که هر ماتریس متعماد ویژه معرف یک دوران است.
مدل مختلط ماتریس متعامد ماتریس یکانی است.
یک ماتریس متعامد ماتریسی خاص از ماتریس واحد است و بنابرین همیشه یک ماتریس نرمال خواهد بود, [ ۱] ماتریس های متعامد کاربردهای نظری و عملی بسیار زیادی دارند. یک ماتریس متعامد n×n یک گروه متعامد ( از گروه های لی ) است که با نماد O ( n ) شناخته می شود و کاربرد زیادی در بخش های مختلف علوم فیزیک و ریاضیات دارد.
بعضی از ماتریس های متعامد به شرح زیرند:
• تبدیل همانی: {\displaystyle {\begin{bmatrix}1& 0\\0& 1\\\end{bmatrix}}}
• دوران به اندازه ۱۶. ۲۶ درجه: {\displaystyle {\begin{bmatrix}0. 96& - 0. 28\\0. 28& \; \; \, 0. 96\\\end{bmatrix}}}
• بازتاب تحت محور xها: {\displaystyle {\begin{bmatrix}1& 0\\0& - 1\\\end{bmatrix}}}
ابتدایی ترین نوع ماتریس های 1×1 ماتریس و هستند.
ماتریس های 2×2 به شکل زیر هستند
به شرط برقراری سه رابطه متعامد هستند:
برای ساختن معادله اول و بدون کاستن از کلیت مسئله می توان فرض کرد p = cos θ و q = sin θ; بنابرین t = − q, u = p or t = q, u = − p. ما می توانیم اولین مورد را به عنوان دوران به اندازه زاویه θ ( که اگرθ = 0 به تبدیل همانی تبدیل می شود ) , و دومین را به عنوان بازتاب تحت خطی به زاویه θ/2.
حالت خاص بازتاب در مورد θ=90° منجر می شود به بازتاب حول خطی که در زاویه ۴۵ درجه است که به خط y=x معروف استیا به عبارت دیگر جای x و y را عوض می کند و به ماتریس تبدیل زیر نیز معروف است:

wiki: ماتریس متعامد
