در نظریه گراف، هر گراف ساده دارای یک یا بیشتر مولفه همبندی ( به انگلیسی: Connected component ) است. یک زیر گراف مانند H از G یک مؤلفهٔ همبندی برای G است اگر و فقط اگر بین هر دو راس در H، دست کم یک مسیر وجود داشته باشد و با افزودن هر راس ( و یا یال ) دیگری از G به H این خاصیت از بین برود. به عبارت دیگر هر زیر گراف بیشینه و همبند از G، یک مؤلفهٔ همبندی G است.
مولفه های همبندی یک گراف، رده های هم ارزی تعریف شده توسط رابطهٔ هم ارزی «قابل دست یابی بودن» ( به انگلیسی: Reachability ) روی راس های گراف هستند. به راحتی می توان دید که رابطهٔ «قابل دست یابی بودن» سه خاصیت انعکاسی، تقارنی و ترایایی را داراست و در نتیجه یک رابطهٔ هم ارزی روی راس های گراف تشکیل می دهد.
بین همهٔ راس هایی که تحت این رابطه در یک رده قرار می گیرند دست کم یک مسیر وجود دارد و با افزودن هر راس دیگری به یک رده این ویژگی از میان می رود پس طبق تعریف، هر رده متناظر با یک مؤلفهٔ همبندی است.
با استفاده از هر روش جستجو در گراف، مانند جستجوی اول سطح یا جستجوی اول عمق، می توان مؤلفه های همبندی یک گراف را پیدا کرد. به عنوان نمونه، برای پیدا کردن تمامی راس هایی که با راس v در یک مؤلفهٔ همبندی قرار دارند می توان جستجوی اول عمق را از راس v شروع کرد و تمامی راس هایی که در طول جستجو به آن ها وارد می شویم در همان مؤلفهٔ همبندی قرار دارند که راس v در آن است.
برای پیدا کردن مؤلفه های همبندی یک گراف، G = ( V , E ) ، نیاز به زمان اجرای خطی نسبت به طول ورودی O ( | V | + | E | ) داریم.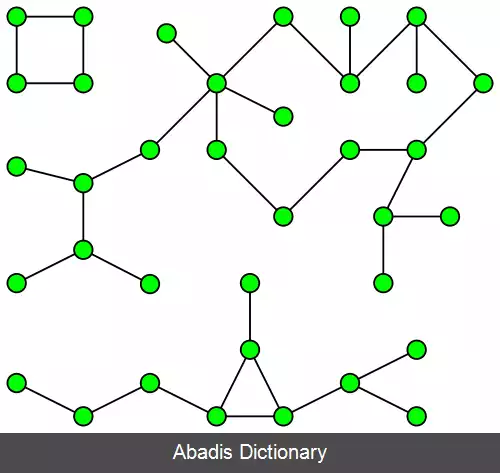
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمولفه های همبندی یک گراف، رده های هم ارزی تعریف شده توسط رابطهٔ هم ارزی «قابل دست یابی بودن» ( به انگلیسی: Reachability ) روی راس های گراف هستند. به راحتی می توان دید که رابطهٔ «قابل دست یابی بودن» سه خاصیت انعکاسی، تقارنی و ترایایی را داراست و در نتیجه یک رابطهٔ هم ارزی روی راس های گراف تشکیل می دهد.
بین همهٔ راس هایی که تحت این رابطه در یک رده قرار می گیرند دست کم یک مسیر وجود دارد و با افزودن هر راس دیگری به یک رده این ویژگی از میان می رود پس طبق تعریف، هر رده متناظر با یک مؤلفهٔ همبندی است.
با استفاده از هر روش جستجو در گراف، مانند جستجوی اول سطح یا جستجوی اول عمق، می توان مؤلفه های همبندی یک گراف را پیدا کرد. به عنوان نمونه، برای پیدا کردن تمامی راس هایی که با راس v در یک مؤلفهٔ همبندی قرار دارند می توان جستجوی اول عمق را از راس v شروع کرد و تمامی راس هایی که در طول جستجو به آن ها وارد می شویم در همان مؤلفهٔ همبندی قرار دارند که راس v در آن است.
برای پیدا کردن مؤلفه های همبندی یک گراف، G = ( V , E ) ، نیاز به زمان اجرای خطی نسبت به طول ورودی O ( | V | + | E | ) داریم.

wiki: مؤلفه همبندی
