قیاس منطقی دست به دست در قضیه با نظریه گراف، یکی از شاخه های ریاضیات، قیاس دست به دست موقعیتی است که در آن هر گراف متناهی غیرجهت دار، تعداد رأس های با درجه فرد آن زوج است. به اصطلاح، در یک مهمانی که افراد با هم دست می دهند، تعداد زوجی از افراد هستند که با تعداد فردی از افراد دیگر دست داده باشند. قیاس منطقی دست به دست نتیجه فرمول مجموع درجه است ( که در بعضی مواقع قیاس منطقی دست به دست نامیده می شود )
در یک گرافی که در آن v راس و E یال می باشد . هر دو نتایج توسط لئونهارد اویلر ( ۱۷۳۶ ) در روزنامه معروف وی در سون بریج کونیگز برگ اثبات گردیدند که سبب آغاز مطالعه نظریه گراف شد. رئوس با درجه فرد در یک گراف در بعضی مواقع گره های فرد یا رئوس فرد نامیده می شوند; در این مجموعه اصطلاحات، قیاس منطقی دست به دست می تواند این توضیح را ارائه دهد که هر گراف زوج تا گره فرد دارد .
اثبات فرمول مجموع درجه اویلر از تکنیک دو بار شمارش استفاده می کند : او تعداد جفتهای وابسته یا متلاقی ( v، e ) را که در آن e یال و v نقطه پایانی هستند به دو صورت شمارش می کند . راس v به جفت ( deg ( v تعلق دارد که در آن ( deg ( v ( درجه v ) تعداد یال های وابسته با آن است. بنابراین تعداد جفتهای وابسته ( متلاقی ) مجموع درجات می باشد. در حالی که، هر یال در نمودار دقیقاً به دو جفت متلاقی متعلق است، برای هر کدام از نقاط پایانی یک جفت وجود دارد، در نتیجه تعداد جفتهای متلاقی۲|E| است . از آنجایی که این دو فرمول عناصر مشابهی را شمارش می کنند باید ارزش های برابر داشته باشند. در یک مجموعه اعداد صحیح، توازن ( زوجیت ) مجموعه با ارقام زوج در جمع تأثیری نمی گذارد ; جمع کل در صورتی زوج می شود که یک تعداد زوج از ارقام فرد وجود داشته باشد و زمانی که یک تعداد فرد از اعداد فرد موجود باشد آنگاه فرد می گردد. از آنجایی که یک طرف فرمول مجموع درجات عدد زوج ۲|E| است، مجموع طرف دیگر باید تعداد زوجی از ارقام فرد را داشته باشد. این بدین معنی است که باید تعداد زوجی از رئوس درجه فرد وجود داشته باشد.
فرمول مجموع درجات این را متذکر می شود که هر گراف های منظم ( r ) با n راس rn/۲ یال دارد. [ ۱] خصوصاً، اگر r فرد است، تعداد یال ها باید به صورت زوج به r بخشپذیر باشند.
قیاس دست به دست به گراف های نامحدود صدق نمی کند، حتی زمانی که آنها تنها یک تعداد متناهی از رئوس درجه فرد دارند. به عنوان مثال، گراف مسیر نامحدود با یک نقطه پایانی تنها دارای یک راس درجه فرد به جای داشتن یک تعداد زوج از رئوس است.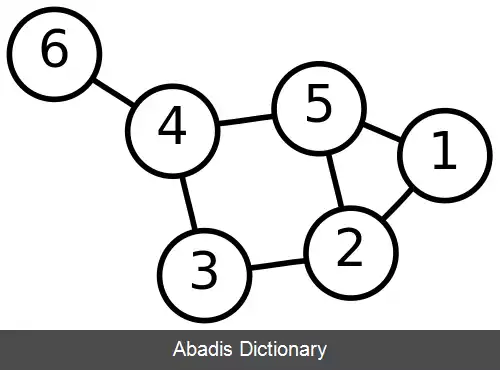
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر یک گرافی که در آن v راس و E یال می باشد . هر دو نتایج توسط لئونهارد اویلر ( ۱۷۳۶ ) در روزنامه معروف وی در سون بریج کونیگز برگ اثبات گردیدند که سبب آغاز مطالعه نظریه گراف شد. رئوس با درجه فرد در یک گراف در بعضی مواقع گره های فرد یا رئوس فرد نامیده می شوند; در این مجموعه اصطلاحات، قیاس منطقی دست به دست می تواند این توضیح را ارائه دهد که هر گراف زوج تا گره فرد دارد .
اثبات فرمول مجموع درجه اویلر از تکنیک دو بار شمارش استفاده می کند : او تعداد جفتهای وابسته یا متلاقی ( v، e ) را که در آن e یال و v نقطه پایانی هستند به دو صورت شمارش می کند . راس v به جفت ( deg ( v تعلق دارد که در آن ( deg ( v ( درجه v ) تعداد یال های وابسته با آن است. بنابراین تعداد جفتهای وابسته ( متلاقی ) مجموع درجات می باشد. در حالی که، هر یال در نمودار دقیقاً به دو جفت متلاقی متعلق است، برای هر کدام از نقاط پایانی یک جفت وجود دارد، در نتیجه تعداد جفتهای متلاقی۲|E| است . از آنجایی که این دو فرمول عناصر مشابهی را شمارش می کنند باید ارزش های برابر داشته باشند. در یک مجموعه اعداد صحیح، توازن ( زوجیت ) مجموعه با ارقام زوج در جمع تأثیری نمی گذارد ; جمع کل در صورتی زوج می شود که یک تعداد زوج از ارقام فرد وجود داشته باشد و زمانی که یک تعداد فرد از اعداد فرد موجود باشد آنگاه فرد می گردد. از آنجایی که یک طرف فرمول مجموع درجات عدد زوج ۲|E| است، مجموع طرف دیگر باید تعداد زوجی از ارقام فرد را داشته باشد. این بدین معنی است که باید تعداد زوجی از رئوس درجه فرد وجود داشته باشد.
فرمول مجموع درجات این را متذکر می شود که هر گراف های منظم ( r ) با n راس rn/۲ یال دارد. [ ۱] خصوصاً، اگر r فرد است، تعداد یال ها باید به صورت زوج به r بخشپذیر باشند.
قیاس دست به دست به گراف های نامحدود صدق نمی کند، حتی زمانی که آنها تنها یک تعداد متناهی از رئوس درجه فرد دارند. به عنوان مثال، گراف مسیر نامحدود با یک نقطه پایانی تنها دارای یک راس درجه فرد به جای داشتن یک تعداد زوج از رئوس است.

wiki: قیاس منطقی دست به دست
