قضیهٔ نمونه برداری نایکوییست - شنون، اساسی ترین قضیه در پردازش سیگنال دیجیتال و مخابرات دیجیتال است. این قضیه شرط امکان بازیابی سیگنال اولیه از نمونه های آن را را بیان می کند و پلی بین سیگنال های دیجیتال و آنالوگ می سازد.
این قضیه بیان می کند که اگر سیگنال x ( t ) سیگنالی با باند محدود باشد، یعنی به ازای | f | ≥ W ، تبدیل فوریه ی آن صفر باشد ( X ( f ) = 0 ) ، در آن صورت اگر آن را با تناوب T s که T s < = 1 2 W است، نمونه برداری کنیم و دنبالهٔ { x ( n T s ) } را به دست آوریم، سیگنال اولیه را می توان از روی نمونه ها به کمک رابطهٔ زیر بازیابی کرد:
∑ n = − ∞ + ∞ 2 T s W ′ x ( n T s ) S i n c
که در آن W ′ عددی است دلخواه که در شرط زیر صدق کند:
W ≤ W ′ ≤ 1 T s − W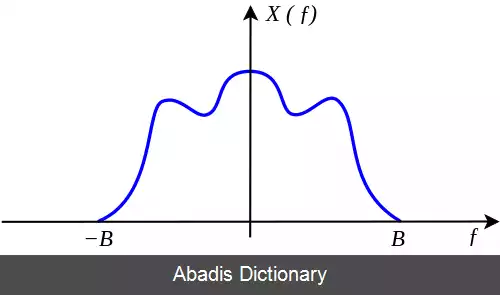
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین قضیه بیان می کند که اگر سیگنال x ( t ) سیگنالی با باند محدود باشد، یعنی به ازای | f | ≥ W ، تبدیل فوریه ی آن صفر باشد ( X ( f ) = 0 ) ، در آن صورت اگر آن را با تناوب T s که T s < = 1 2 W است، نمونه برداری کنیم و دنبالهٔ { x ( n T s ) } را به دست آوریم، سیگنال اولیه را می توان از روی نمونه ها به کمک رابطهٔ زیر بازیابی کرد:
∑ n = − ∞ + ∞ 2 T s W ′ x ( n T s ) S i n c
که در آن W ′ عددی است دلخواه که در شرط زیر صدق کند:
W ≤ W ′ ≤ 1 T s − W

