قضیه مِنِلائوس از قضایای مهم هندسه است که بیان می دارد چنانچه خطی ( در شکل EF ) دو ضلع مثلثی ( مثلث ABC در شکل ) را قطع کند آنگاه رابطۀ زیر برای آن برقرار است:
A F F B × B D D C × C E E A = − 1. یا به صورت دیگر:
A F × B D × C E = − F B × D C × E A .
این قضیه از پاره خط های علامتدار استفاده می کند. به عبارت دیگر طول پاره خط AB با توجه به اینکه نقطۀ A سمت راست B قرار دارد می تواند مثبت یا منفی تعریف شود. مثلا اگر F بین A و B باشد، نسبت AF به FB مثبت می شود و در غیر این صورت این مقدار منفی می شود.
عکس قضیه نیز برقرار است:
اگر نقاط D , E, F طوری روی اضلاع مثلث انتخاب شوند که رابطۀ زیر برقرار باشد:
A F F B × B D D C × C E E A = − 1. آنگاه نقاط D , E , F هم خط هستند. قضیه منلائوس شباهت زیادی به قضیه سوا دارد.
منلائوس آن را در کتابش با نام Sphaerica نوشته است. این قضیه از مبانی مثلثات کروی می باشد.
از ریاضی دانان مسلمان و ایرانی ثابت ابن قره نخستین بار در مورد این قضیه اثر لمعه ارشمیدس را ترجمه کرده خواجه نصیر الدین طوسی بر آن شرحی نوشت .
بعدها ابوالحسن علی بن احمد نسوی نیز در کتاب خود الاشباع این شرح را ادامه داد. [ ۲]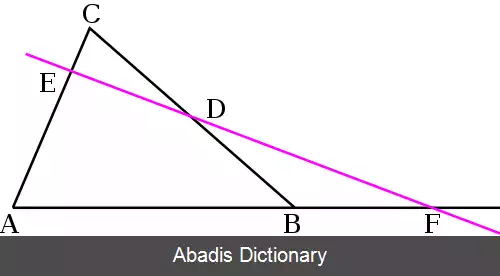
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفA F F B × B D D C × C E E A = − 1. یا به صورت دیگر:
A F × B D × C E = − F B × D C × E A .
این قضیه از پاره خط های علامتدار استفاده می کند. به عبارت دیگر طول پاره خط AB با توجه به اینکه نقطۀ A سمت راست B قرار دارد می تواند مثبت یا منفی تعریف شود. مثلا اگر F بین A و B باشد، نسبت AF به FB مثبت می شود و در غیر این صورت این مقدار منفی می شود.
عکس قضیه نیز برقرار است:
اگر نقاط D , E, F طوری روی اضلاع مثلث انتخاب شوند که رابطۀ زیر برقرار باشد:
A F F B × B D D C × C E E A = − 1. آنگاه نقاط D , E , F هم خط هستند. قضیه منلائوس شباهت زیادی به قضیه سوا دارد.
منلائوس آن را در کتابش با نام Sphaerica نوشته است. این قضیه از مبانی مثلثات کروی می باشد.
از ریاضی دانان مسلمان و ایرانی ثابت ابن قره نخستین بار در مورد این قضیه اثر لمعه ارشمیدس را ترجمه کرده خواجه نصیر الدین طوسی بر آن شرحی نوشت .
بعدها ابوالحسن علی بن احمد نسوی نیز در کتاب خود الاشباع این شرح را ادامه داد. [ ۲]

wiki: قضیه منلائوس
