در آنالیز ریاضی، قضیه مقدار میانی یا قضیه بولتسانو بیان می کند که برای هر تابع پیوسته f روی بازهٔ ، به ازای هر مقدار u که میان f ( a ) و f ( b ) و یا برابر آنان باشد، حداقل یک عدد مانند c در بازه وجود دارد که f ( c ) = u . [ ۱]
حالتی از این قضیه نخستین بار توسط برنارد بولتسانو اثبات شد که برای وجود ریشه بین دو مقدار مثبت و منفی بیان می شود: اگر برای تابع f ، پیوسته روی ، داشته باشیم f ( a ) f ( b ) < 0 ، آنگاه وجود دارد حداقل یک مقدار چون c ∈ به طوری که f ( c ) = 0 . [ ۲]
قضیه ای با نام مشابه برای انتگرال ها وجود ندارد. این قضیه را نباید با قضیه مقدار میانگین اشتباه بگیریم.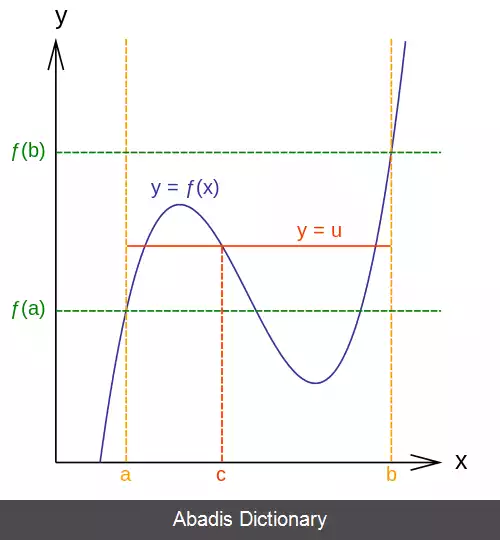
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفحالتی از این قضیه نخستین بار توسط برنارد بولتسانو اثبات شد که برای وجود ریشه بین دو مقدار مثبت و منفی بیان می شود: اگر برای تابع f ، پیوسته روی ، داشته باشیم f ( a ) f ( b ) < 0 ، آنگاه وجود دارد حداقل یک مقدار چون c ∈ به طوری که f ( c ) = 0 . [ ۲]
قضیه ای با نام مشابه برای انتگرال ها وجود ندارد. این قضیه را نباید با قضیه مقدار میانگین اشتباه بگیریم.

wiki: قضیه مقدار میانی
