قضیهٔ سوا، قضیه ای در هندسهٔ دوبعدی است؛ به این ترتیب که اگر مثلث دلخواه ABC را در نظر بگیریم و نقاط F و E، D را به ترتیب روی اضلاع AB و CA، BC انتخاب کنیم، خط های CF و BE و AD یکدیگر را در یک نقطه قطع می کنند اگر و فقط اگر:
در حالی که AF فاصلهٔ مستقیم بین دو نقطهٔ A و F است. ( فاصله در یک جهت روی یک خط مثبت و در جهت مخالف منفی در نظر گرفته می شود )
شکل دیگر قضیهٔ سوا به این شکل است: که می گوییم سه خط CF و BE و AD یکدیگر را در یک نقطه قطع می کنند، اگر و فقط اگر:
این قضیه توسط جووانی سوا ( Giovanni Ceva ) در اثرش به نام De lineis rectis، که در سال ۱۶۷۸ نوشت، اثبات شده بود اما پیش از او یوسف بن احمد مؤتمن بن هود، پادشاه ساراگوسا در قرن یازدهم، آن را اثبات کرده بود.
مثلث DEF را مثلث سوایی O و خط های CF و BE و AD را سوایی های O می نامند.
فرض کنید: A D و B E و C F در نقطه ای مانند O یکدیگر را قطع می کنند. چون مثلث های △ B O D و △ C O D ارتفاع یکسان دارند، خواهیم داشت:
به دلیل مشابه:
در ادامهٔ مطلب بالا خواهیم داشت:
همچنین
و
با ضرب این سه عبارت در یکدیگر خواهیم داشت:
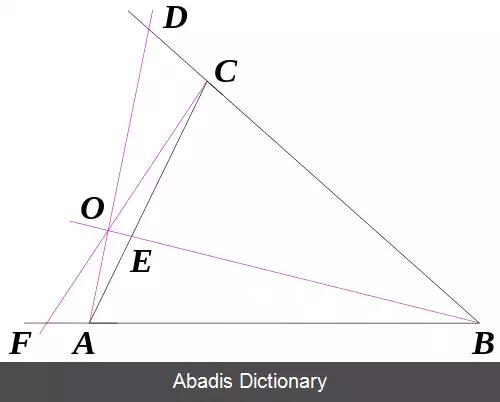
برای اثبات عکس قضیه، فرض کنید نقاط D و E و F به گونه ای اند که رابطهٔ بالا را برقرار می کنند؛ حال فرض کنید که A D و B E در نقطه O با یکدیگر برخورد می کنند ولی امتداد C O ضلع A B را در نقطهٔ دیگری به نام F ′ قطع می کند. با توجه به اثباتی که در بالا کردیم باید داشته باشیم:
با مقایسهٔ دو رابطه خواهیم داشت:
یک یکم ( ۱/۱ ) را به دو طرف تساوی اضافه می کنیم، می شود: A F ′ + F ′ B = A F + F B = A B ( حالت یکم ) یا با کم کردن یک از آن می شود: F ′ B − A F ′ = F B − A F = A B ( حالت دوم ) ، خواهیم داشت:
بنابراین F ′ B = F B در نتیجه F و F ′ بر روی هم قرار دارند، پس A D و B E و C F = C F ′ در نقطهٔ O یکدیگر را قطع می کنند؛ هر دو سوی قضیه اثبات شد.
برای شکل مثلثی این قضیه، یک رویکرد این است که نگاه کنیم که سه سوایی متقاطع در نقطهٔ O، مثلث △ A B C را به سه مثلث کوچکتر △ A O B و △ B O C و △ C O A تقسیم می کنند. با استفاده از قانون سینوس ها برای هر مثلث خواهیم داشت:
اگر سه رابطه را در یکدیگر ضرب کنیم می بینیم که سمت راست آن برابر با ۱ و سمت چپ آن برابر با عبارت داده شده در قضیه خواهد شد.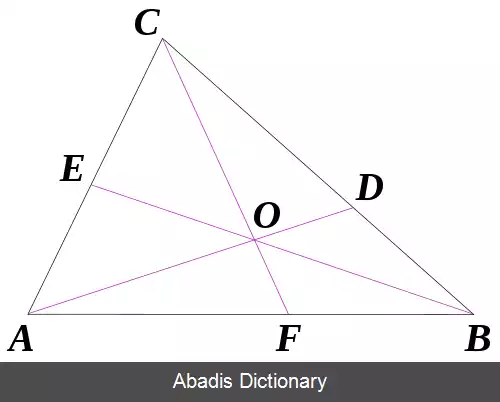
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر حالی که AF فاصلهٔ مستقیم بین دو نقطهٔ A و F است. ( فاصله در یک جهت روی یک خط مثبت و در جهت مخالف منفی در نظر گرفته می شود )
شکل دیگر قضیهٔ سوا به این شکل است: که می گوییم سه خط CF و BE و AD یکدیگر را در یک نقطه قطع می کنند، اگر و فقط اگر:
این قضیه توسط جووانی سوا ( Giovanni Ceva ) در اثرش به نام De lineis rectis، که در سال ۱۶۷۸ نوشت، اثبات شده بود اما پیش از او یوسف بن احمد مؤتمن بن هود، پادشاه ساراگوسا در قرن یازدهم، آن را اثبات کرده بود.
مثلث DEF را مثلث سوایی O و خط های CF و BE و AD را سوایی های O می نامند.
فرض کنید: A D و B E و C F در نقطه ای مانند O یکدیگر را قطع می کنند. چون مثلث های △ B O D و △ C O D ارتفاع یکسان دارند، خواهیم داشت:
به دلیل مشابه:
در ادامهٔ مطلب بالا خواهیم داشت:
همچنین
و
با ضرب این سه عبارت در یکدیگر خواهیم داشت:
برای اثبات عکس قضیه، فرض کنید نقاط D و E و F به گونه ای اند که رابطهٔ بالا را برقرار می کنند؛ حال فرض کنید که A D و B E در نقطه O با یکدیگر برخورد می کنند ولی امتداد C O ضلع A B را در نقطهٔ دیگری به نام F ′ قطع می کند. با توجه به اثباتی که در بالا کردیم باید داشته باشیم:
با مقایسهٔ دو رابطه خواهیم داشت:
یک یکم ( ۱/۱ ) را به دو طرف تساوی اضافه می کنیم، می شود: A F ′ + F ′ B = A F + F B = A B ( حالت یکم ) یا با کم کردن یک از آن می شود: F ′ B − A F ′ = F B − A F = A B ( حالت دوم ) ، خواهیم داشت:
بنابراین F ′ B = F B در نتیجه F و F ′ بر روی هم قرار دارند، پس A D و B E و C F = C F ′ در نقطهٔ O یکدیگر را قطع می کنند؛ هر دو سوی قضیه اثبات شد.
برای شکل مثلثی این قضیه، یک رویکرد این است که نگاه کنیم که سه سوایی متقاطع در نقطهٔ O، مثلث △ A B C را به سه مثلث کوچکتر △ A O B و △ B O C و △ C O A تقسیم می کنند. با استفاده از قانون سینوس ها برای هر مثلث خواهیم داشت:
اگر سه رابطه را در یکدیگر ضرب کنیم می بینیم که سمت راست آن برابر با ۱ و سمت چپ آن برابر با عبارت داده شده در قضیه خواهد شد.


wiki: قضیه سوا
