قضیه جوجه اردک زشت یک استدلال است که نشان می دهد طبقه بندی بدون جهت گیری غیرممکن است. به طور دقیق تر این قضیه تعداد محدودی از ویژگی ها را در نظر می گیرد که با اتصالات منطفی با هم ترکیب می شوند و ادعا می کند که هر دو شی متفاوت تعداد برابری از ویژگی های مشابه دارند.
این قضیه با الهام از داستان «جوجه اردک زشت» از هانس کریستیان آندرسن از سال۱۸۴۳ میلادی نام گذاری شده است زیرا ادعا می کند که یک جوجه اردک به همان اندازه ای شبیه یک قو است که دو قو شبیه به یک دیگر هستند. این قضیه توسط ساتوشی واتانابه در سال 1969 میلادی به دست آمد. [ ۱]
فرض کنیم که n شی در جهان وجود داشته باشد. حال اگر یک شخص می خواهد این اشیا را دسته بندی کند بدون اینکه هیچ گونه سوگیری یا حسی در مورد اینکه چه دسته بندی طبیعی است داشته باشد. برای این کار شخص تمام دسته بندی های ممکن این اشیا را بررسی می کند. تمام حالات زیرمجموعه گیری از این n شی برابر است با اندازه زیرمجموعه توانی این n شی که برابر است با 2 n . حال شخص می تواند بررسی کند که دو شی چند زیرمجموعه مشترک دارند تا میزان شباهت آن ها را مشخص کند. اما شخص به نتیجه ای نمی رسد زیرا هر دو شی دقیقا به یک اندازه در زیرمجوعه ها ظاهر شده اند. به طور دقیق تر این اشیا در 2 n − 1 دسته ( نصف تعداد کل دسته ها ) دقیقا مشاهده شده اند.
برای اینکه شخص این موضوع را متوجه شود می تواند هر دسته را به شکل یک رشته در نظر بگیرد که برای هر شی که در این دسته نیست 0 و برای هر شی که در این دسته وجود دارد 1 در جایگاه آن درج شده است. مشخص است که 2 n رشته در کل وجود دارد.
هر دو بیت دقیقا در نیمی از کل حالات با هم مطابقت دارند. شخص ممکن است که دو شی را انتخاب کند و بیت های رشته را دوباره مرتب کند تا این دو بیت در ابتدا قرار بگیرند. همچنین فرض می کند که اعداد به ترتیب الفبایی مرتب شده اند.
2 n / 2 عدد اول بیت اولشان 0 و 2 n / 2 عدد دوم بیت اولشان 1 است. بین آن ها نیز 2 n / 4 عدد اول بیت اولشان 0 و 2 n / 4 عدد دوم بیت اولشان 1 است. پس صرف نظر ازین که شخص کدام دو شی را انتخاب کند همیشه در نصف دسته ها باهم مطابقت دارند.
در نتیجه اگر ما سوگیری نداشته باشیم که کدام دسته ها بهتر اند، همه اشیا به یک اندازه بهم شبیه خواهند بود ( یا به یک اندازه متفاوت خواهند بود ) . به بیان دیگر تعداد ویژگی هایی که به شکل همزمان دو شی غیر یکسان را در بر دارد برای همه زوج شی ها یکسان است.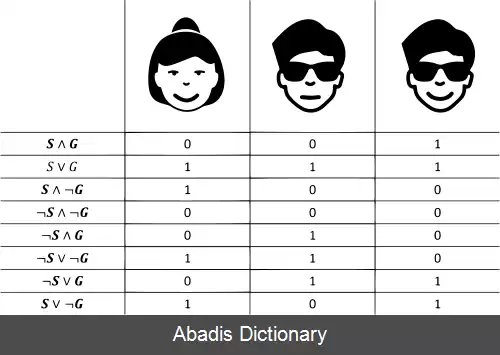
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین قضیه با الهام از داستان «جوجه اردک زشت» از هانس کریستیان آندرسن از سال۱۸۴۳ میلادی نام گذاری شده است زیرا ادعا می کند که یک جوجه اردک به همان اندازه ای شبیه یک قو است که دو قو شبیه به یک دیگر هستند. این قضیه توسط ساتوشی واتانابه در سال 1969 میلادی به دست آمد. [ ۱]
فرض کنیم که n شی در جهان وجود داشته باشد. حال اگر یک شخص می خواهد این اشیا را دسته بندی کند بدون اینکه هیچ گونه سوگیری یا حسی در مورد اینکه چه دسته بندی طبیعی است داشته باشد. برای این کار شخص تمام دسته بندی های ممکن این اشیا را بررسی می کند. تمام حالات زیرمجموعه گیری از این n شی برابر است با اندازه زیرمجموعه توانی این n شی که برابر است با 2 n . حال شخص می تواند بررسی کند که دو شی چند زیرمجموعه مشترک دارند تا میزان شباهت آن ها را مشخص کند. اما شخص به نتیجه ای نمی رسد زیرا هر دو شی دقیقا به یک اندازه در زیرمجوعه ها ظاهر شده اند. به طور دقیق تر این اشیا در 2 n − 1 دسته ( نصف تعداد کل دسته ها ) دقیقا مشاهده شده اند.
برای اینکه شخص این موضوع را متوجه شود می تواند هر دسته را به شکل یک رشته در نظر بگیرد که برای هر شی که در این دسته نیست 0 و برای هر شی که در این دسته وجود دارد 1 در جایگاه آن درج شده است. مشخص است که 2 n رشته در کل وجود دارد.
هر دو بیت دقیقا در نیمی از کل حالات با هم مطابقت دارند. شخص ممکن است که دو شی را انتخاب کند و بیت های رشته را دوباره مرتب کند تا این دو بیت در ابتدا قرار بگیرند. همچنین فرض می کند که اعداد به ترتیب الفبایی مرتب شده اند.
2 n / 2 عدد اول بیت اولشان 0 و 2 n / 2 عدد دوم بیت اولشان 1 است. بین آن ها نیز 2 n / 4 عدد اول بیت اولشان 0 و 2 n / 4 عدد دوم بیت اولشان 1 است. پس صرف نظر ازین که شخص کدام دو شی را انتخاب کند همیشه در نصف دسته ها باهم مطابقت دارند.
در نتیجه اگر ما سوگیری نداشته باشیم که کدام دسته ها بهتر اند، همه اشیا به یک اندازه بهم شبیه خواهند بود ( یا به یک اندازه متفاوت خواهند بود ) . به بیان دیگر تعداد ویژگی هایی که به شکل همزمان دو شی غیر یکسان را در بر دارد برای همه زوج شی ها یکسان است.

wiki: قضیه جوجه اردک زشت
