قضیه آپولونیوس. در هندسه اقلیدسی ، قضیه آپولونیوس قضیه ای است که طول میانه ی یک مثلث را به طول اضلاع آن مرتبط می سازد. این قضیه بیان می دارد که "جمع مربع دو ضلع از هر مثلث، دو برابر جمع مربع نصف ضلع سوم و مربع میانه وارد بر ضلع سوم است".
به طور خاص و دقیق تر، اگر مثلث دلخواه A B C داده شده باشد، به گونه ای که A D میانه ی وارد بر B C باشد، آنگاه طبق این قضیه خواهیم داشت:
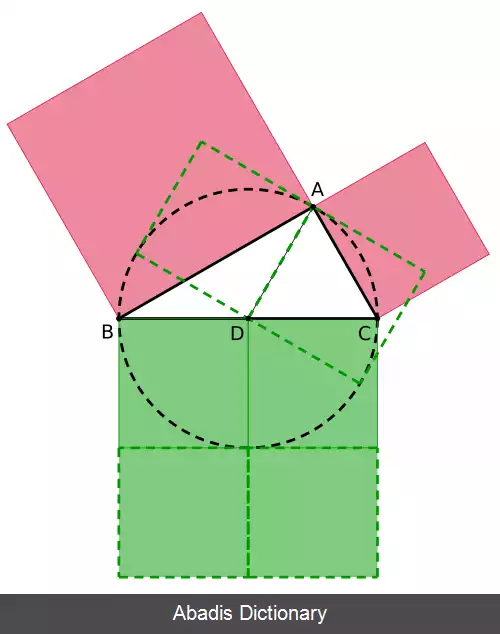
این قضیه حالت خاصی از قضیه استوارت است. برای یک مثلث متساوی الساقین با |AB| = |AC|، میانه A D عمود بر B C است و این قضیه در این حالت به قضیه فیثاغورث برای مثلث A D B ( یا مثلث A D C ) تقلیل پیدا می کند. ازین حقیقت که قطر های یک متوازی الاضلاع همدیگر را به طور مساوی قطع می کنند بهره گرفته و نشان داده می شود که قضیه آپولونیوس با قانون متوازی الاضلاع معادل است.
این قضیه به افتخار آپولونیوس از شهر پرگا، به نام قضیه آپولونیوس نام گذاری شده است.
این قضیه را می توان به صورت حالت خاصی از قضیه استوارت اثبات کرد، یا می توان آن را به کمک بردار ها ( قانون متوازی الاضلاع را ببینید ) اثبات نمود. در ادامه، اثبات مستقلی به کمک قانون کسینوس ها آورده می شود. [ ۱]
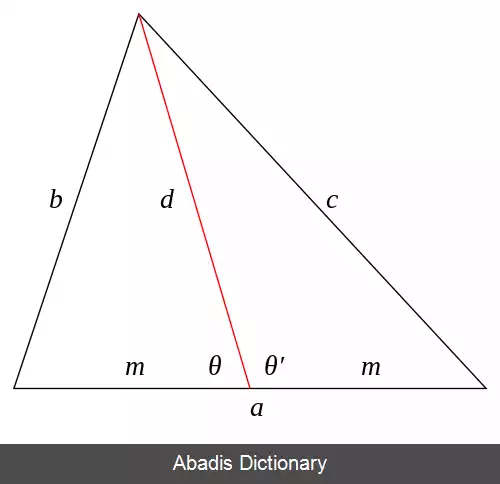
فرض کنید مثلث دلخواهی داریم با اضلاع a , b , c که طول میانه وارد بر ضلع a آن h باشد. فرض کنید m طول پاره خطی از a باشد که توسط میانه وارد بر آن ایجاد شده است، بنابر این m نصف a خواهد بود. فرض کنید زوایای تشکیل شده بین a و d که شامل b و c هستند به ترتیب θ و θ ′ باشند. آنگاه θ ′ مکمل θ بوده و c o s ( θ ′ ) = − c o s ( θ ) .
حال طبق قانون کسینوس ها برای θ و θ ′ داریم:
که با اضافه کردن اولین و سومین معادله می رسیم به:
که همان حکم مطلوب است.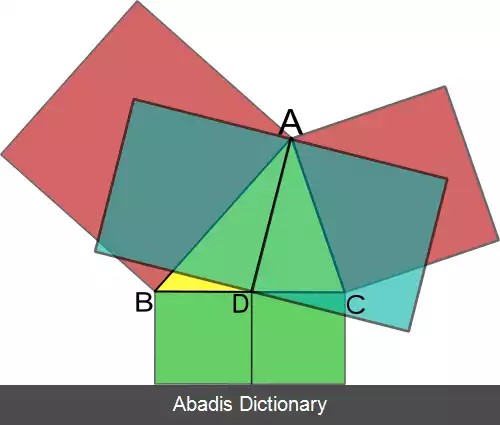
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبه طور خاص و دقیق تر، اگر مثلث دلخواه A B C داده شده باشد، به گونه ای که A D میانه ی وارد بر B C باشد، آنگاه طبق این قضیه خواهیم داشت:
این قضیه حالت خاصی از قضیه استوارت است. برای یک مثلث متساوی الساقین با |AB| = |AC|، میانه A D عمود بر B C است و این قضیه در این حالت به قضیه فیثاغورث برای مثلث A D B ( یا مثلث A D C ) تقلیل پیدا می کند. ازین حقیقت که قطر های یک متوازی الاضلاع همدیگر را به طور مساوی قطع می کنند بهره گرفته و نشان داده می شود که قضیه آپولونیوس با قانون متوازی الاضلاع معادل است.
این قضیه به افتخار آپولونیوس از شهر پرگا، به نام قضیه آپولونیوس نام گذاری شده است.
این قضیه را می توان به صورت حالت خاصی از قضیه استوارت اثبات کرد، یا می توان آن را به کمک بردار ها ( قانون متوازی الاضلاع را ببینید ) اثبات نمود. در ادامه، اثبات مستقلی به کمک قانون کسینوس ها آورده می شود. [ ۱]
فرض کنید مثلث دلخواهی داریم با اضلاع a , b , c که طول میانه وارد بر ضلع a آن h باشد. فرض کنید m طول پاره خطی از a باشد که توسط میانه وارد بر آن ایجاد شده است، بنابر این m نصف a خواهد بود. فرض کنید زوایای تشکیل شده بین a و d که شامل b و c هستند به ترتیب θ و θ ′ باشند. آنگاه θ ′ مکمل θ بوده و c o s ( θ ′ ) = − c o s ( θ ) .
حال طبق قانون کسینوس ها برای θ و θ ′ داریم:
که با اضافه کردن اولین و سومین معادله می رسیم به:
که همان حکم مطلوب است.



wiki: قضیه آپولونیوس
