قضیه اصلی (تحلیل الگوریتم ها). در تحلیل الگوریتم ها، قضیه اصلی برای تحلیل مجانبی بسیاری از الگوریتم های تقسیم و حل استفاده می شود. در این نوع از الگوریتم ها معمولاً می توان یک رابطهٔ بازگشتی برای توصیف زمان اجرای آنها پیدا کرد. برای توصیف پیچیدگی چنین رابطه ای ( به کمک نماد Θ ) از این قضیه استفاده می شود.
البته نمی توان هر رابطهٔ بازگشتی را به کمک این قضیه حل کرد. روش اکرا - بازی تعمیمی از این قضیه است. این قضیه با کتاب معروف مقدمه ای بر الگوریتم ها به شهرت رسید.
قضیه اصلی یک روش سرراست برای حل روابط بازگشتی به فرم زیر ارائه می کند:
T ( n ) = a T ( ) + f ( n )
با فرض این که b > 1 و a > 0 و f ( n ) ⩾ 0 باشند.
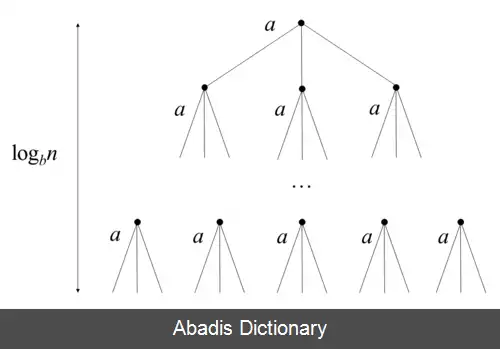
این رابطهٔ بازگشتی زمان اجرای الگوریتمی را توصیف می کند T ( n ) که مسأله ای به اندازهٔ n را به a زیرمسأله ( همگی به اندازهٔ تقریبی n b ) تقسیم می کند. همچنین f ( n ) هزینهٔ تقسیم و ترکیب زیرمسائل است.
مقدار توان بحرانی c crit را به صورت c crit = log b a تعریف می کنیم. در این صورت قضیه اصلی بیان می کند که:[ ۱]
توجه کنید این سه حالت بعضی حالت های ممکن برای f ( n ) را پوشش نمی دهند. یک شکاف بین حالت ۲ و ۳ ( و همچنین بین حالات ۱ و ۲ ) وجود دارد. به عنوان مثال f = n c crit lg n بین حالات ۲ و ۳ قرار می گیرد ( یا f = n c crit / lg n بین ۱ و ۲ ) . این شکاف زمانی پیش می آید که f ( n ) از n c crit بزرگتر ( یا کوچکتر ) باشد ولی مقدار بزرگتر ( یا کوچکتر ) بودنش به صورت چندجمله ای نباشد. در این صورت گاهی می توان از یک تعمیم کوچک برای حالت ۲ استفاده کرد:[ ۲]
برای پیدا کردن پیچیدگی جستجوی دودویی یا مرتب سازی ادغامی و بسیاری از الگوریتم های دیگر می توان از این قضیه استفاده کرد.
T ( n ) = 8 T ( n 2 ) + 1000 n 2
همان طور که در فرمول فوق دیده می شود، متغیرها دارای مقادیر زیر هستند:
a = 8 ، b = 2 ، f ( n ) = 1000 n 2 ، log b a = log 2 8 = 3
حال باید برقراری معادلهٔ زیر را بررسی کنیم:
f ( n ) = O ( n log b a − ϵ )
اگر مقادیر متغیرها را در این رابطه جایگزین کنیم، خواهیم داشت:
1000 n 2 = O ( n 3 − ϵ )
با انتخاب ϵ = 1 داریم:
1000 n 2 = O ( n 3 − 1 ) = O ( n 2 )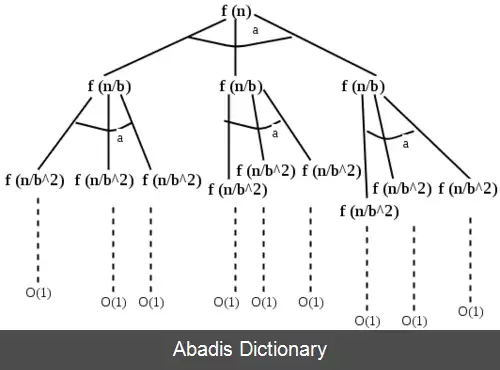

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفالبته نمی توان هر رابطهٔ بازگشتی را به کمک این قضیه حل کرد. روش اکرا - بازی تعمیمی از این قضیه است. این قضیه با کتاب معروف مقدمه ای بر الگوریتم ها به شهرت رسید.
قضیه اصلی یک روش سرراست برای حل روابط بازگشتی به فرم زیر ارائه می کند:
T ( n ) = a T ( ) + f ( n )
با فرض این که b > 1 و a > 0 و f ( n ) ⩾ 0 باشند.
این رابطهٔ بازگشتی زمان اجرای الگوریتمی را توصیف می کند T ( n ) که مسأله ای به اندازهٔ n را به a زیرمسأله ( همگی به اندازهٔ تقریبی n b ) تقسیم می کند. همچنین f ( n ) هزینهٔ تقسیم و ترکیب زیرمسائل است.
مقدار توان بحرانی c crit را به صورت c crit = log b a تعریف می کنیم. در این صورت قضیه اصلی بیان می کند که:[ ۱]
توجه کنید این سه حالت بعضی حالت های ممکن برای f ( n ) را پوشش نمی دهند. یک شکاف بین حالت ۲ و ۳ ( و همچنین بین حالات ۱ و ۲ ) وجود دارد. به عنوان مثال f = n c crit lg n بین حالات ۲ و ۳ قرار می گیرد ( یا f = n c crit / lg n بین ۱ و ۲ ) . این شکاف زمانی پیش می آید که f ( n ) از n c crit بزرگتر ( یا کوچکتر ) باشد ولی مقدار بزرگتر ( یا کوچکتر ) بودنش به صورت چندجمله ای نباشد. در این صورت گاهی می توان از یک تعمیم کوچک برای حالت ۲ استفاده کرد:[ ۲]
برای پیدا کردن پیچیدگی جستجوی دودویی یا مرتب سازی ادغامی و بسیاری از الگوریتم های دیگر می توان از این قضیه استفاده کرد.
T ( n ) = 8 T ( n 2 ) + 1000 n 2
همان طور که در فرمول فوق دیده می شود، متغیرها دارای مقادیر زیر هستند:
a = 8 ، b = 2 ، f ( n ) = 1000 n 2 ، log b a = log 2 8 = 3
حال باید برقراری معادلهٔ زیر را بررسی کنیم:
f ( n ) = O ( n log b a − ϵ )
اگر مقادیر متغیرها را در این رابطه جایگزین کنیم، خواهیم داشت:
1000 n 2 = O ( n 3 − ϵ )
با انتخاب ϵ = 1 داریم:
1000 n 2 = O ( n 3 − 1 ) = O ( n 2 )



