قضیه استوارت، ( به انگلیسی: Stewart's theorem ) در هندسه اندازه پاره خط وارد از یک رأس بر ضلع روبرو را بر حسب اندازه اضلاع مثلث و دو پاره خط ایجاد شده بر روی ضلع می دهد. به افتخار ریاضیدان اسکاتلندی متیو استوارت که در مقاله ای در سال ۱۷۴۸ این قضیه را منتشر کرد، این قضیه را قضیه استوارت نامیده اند. [ ۱]
اگر b ، a و c طول اضلاع مثلت و p طول پاره خط مورد نظر باشد، آنگاه:
a ( p 2 + x y ) = b 2 x + c 2 y و یا:
a p 2 = b 2 x + c 2 y − a x y
که x و y طول دو پاره خط ایجاد شده بر ضلع هستند.
اگر محل برخورد پاره خط p و ضلع BC را P بنامیم، آنگاه بنابر قانون کسینوس ها برای دو زاویه APB و APC داریم:
b 2 = p 2 + y 2 − 2 p y cos θ
c 2 = p 2 + x 2 + 2 p x cos θ
با ضرب کردن x در جمله اول و y در جمله دوم معادلات زیر بدست می آید:
x b 2 = x p 2 + x y 2 − 2 p x y cos θ
y c 2 = y p 2 + y x 2 + 2 p x y cos θ
حال با جمع کردن دو معادله بالا بدست می آید:
x b 2 + y c 2 = ( x + y ) p 2 + x y ( x + y )
که همان معادله قضیه استوارت است.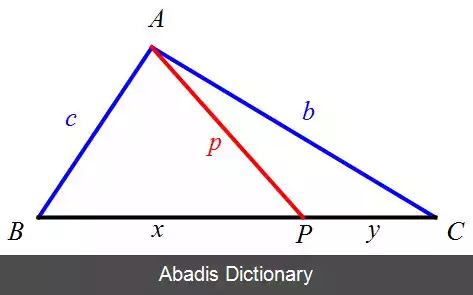
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاگر b ، a و c طول اضلاع مثلت و p طول پاره خط مورد نظر باشد، آنگاه:
a ( p 2 + x y ) = b 2 x + c 2 y و یا:
a p 2 = b 2 x + c 2 y − a x y
که x و y طول دو پاره خط ایجاد شده بر ضلع هستند.
اگر محل برخورد پاره خط p و ضلع BC را P بنامیم، آنگاه بنابر قانون کسینوس ها برای دو زاویه APB و APC داریم:
b 2 = p 2 + y 2 − 2 p y cos θ
c 2 = p 2 + x 2 + 2 p x cos θ
با ضرب کردن x در جمله اول و y در جمله دوم معادلات زیر بدست می آید:
x b 2 = x p 2 + x y 2 − 2 p x y cos θ
y c 2 = y p 2 + y x 2 + 2 p x y cos θ
حال با جمع کردن دو معادله بالا بدست می آید:
x b 2 + y c 2 = ( x + y ) p 2 + x y ( x + y )
که همان معادله قضیه استوارت است.

wiki: قضیه استوارت
