قانون کتانژانت ها

در مثلثات، قانون کتانژانت ها به رابطه میان اندازه ضلع های یک مثلث و کتانژانت نصف سه زاویه آن گفته می شود. سه مقداری که برابریشان در قانون کتانژانت ها ثابت می شود، برابر با شعاع دایره محاطی مثلث مورد نظر هستند.
این قانون اولین بار در قرن نهم میلادی توسط ابن هیثم مطرح گردید[ ۱]
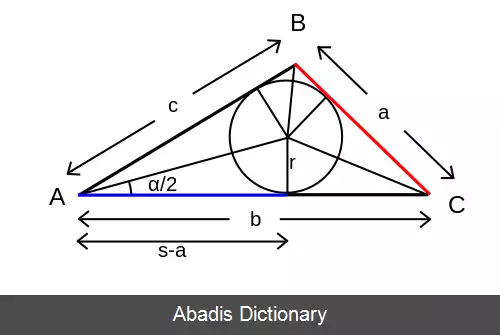
با استفاده از نام گذاری متداول برای مثلث ( مانند شکل روبرو ) که a و b و c ضلع ها، A و B و C رأس ها و α و β و γ زاویه های مثلث، s نصف محیط مثلث ( که مقدار آن برابر s = ( a+b+c ) /2 است ) و r شعاع دایره محاطی هستند، قانون کتانژانت ها به صورت زیر بیان می شود:
و شعاع دایره محاطی از رابطه زیر به دست می آید:
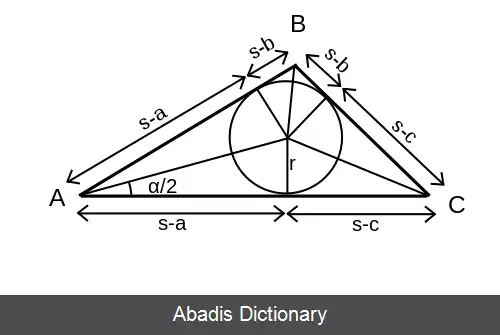
نقطه تماس دایره محاطی با هر ضلع، آن را به دو بخش تقسیم می کند. هر دو بخش مجاور یک رأس با یکدیگر برابر هستند. اگر از هر جفت مجاور یک رأس، یکی انتخاب شود، مجموع این سه برابر s نصف محیط مثلث است. برای نمونه، جمع دو خط آبی و قرمز در شکل روبرو برابر s می باشد. اکنون با استفاده از تعریف تابع کتانژانت، داریم:
رابطه مشابهی برای دو زاویه دیگر به دست می آید. به این ترتیب، بخش اول قانون کتانژانت ها ثابت می شود.
برای بخش دوم، از اتحاد جمع دو زاویه بهره می بریم:
از آن جایی که cot ⁡ ( α / 2 + β / 2 + γ / 2 ) = cot ⁡ ( π / 2 ) = 0 ، رابطه بالا به صورت زیر در می آید:
با جایگذاری مقادیر به دست آمده از بخش اول، نتیجه می شود:
طرف راست رابطه بالا برابر s/r است. به این ترتیب، بخش دوم قانون کتانژانت ها ثابت می شود.
چند رابطه دیگر، از قانون کتانژانت ها به دست می آیند:
• فرمول هرون. مثلث ABC به ۶ مثلث قائم الزاویه کوچکتر، تقسیم می شود. هر دو مثلث مجاور یک رأس، دارای قاعده و ارتفاع برابر با یکدیگر هستند. مثلاً دو مثلث مجاور رأس A دارای قاعده s - a و ارتفاع r هستند. بنابراین مساحت آن مثلث، 1 2 r ( s − a ) {\displaystyle {\tfrac {1}{2}}r ( s - a ) } و مساحت دو مثلث مجاور ( r ( s - a است. به این ترتیب، مساحت مثلث ABC از رابطه زیر محاسبه می شود:
که فرمول هرون را نتیجه می دهد:
• فرمول اول مولواید: از اتحاد جمع دو زاویه و قانون کتانژانت ها داریم:
که نتیجه می دهد:
• فرمول دوم مولواید: از اتحاد جمع دو زاویه و قانون کتانژانت ها داریم:
اکنون، پس از تبدیل ضرب به جمع، رابطه زیر به دست می آید: