در علم مواد، قانون عمومی مخلوط ها، به میانگین وزنی گفته می شود که برای پیش بینی ویژگی های مختلف مواد کامپوزیتی ساخته شده از الیاف پیوسته و تک جهت استفاده می شود. [ ۱] [ ۲] [ ۳] این قانون به صورت تئوری، برای ویژگی هایی مثل مدول الاستیک، دانسیته جرمی، استحکام کششی نهایی، رسانندگی گرمایی و رسانندگی الکتریکی، یک کران بالا و یک کران پایین را تعیین می کند. [ ۳] برای تعیین این مقادیر به طور کلی دو مدل وجود دارد: یکی برای بارگذاری محوری ( مدل Voigt ) , [ ۲] [ ۴] و دیگری برای بارگذاری عرضی ( مدل Reuss ) . [ ۲] [ ۵]
برای یک ویژگی ماده مثل E ( که اغلب مدول الاستیک[ ۱] است ) ، قانون مخلوط ها بیان می کند که اندازهٔ کلی ویژگی در جهت موازی با الیاف، می تواند حداکثر برابر مقدار زیر باشد:
E c = f E f + ( 1 − f ) E m
که در آن
• f = V f V f + V m {\displaystyle f={\frac {V_{f}}{V_{f}+V_{m}}}} کسر حجمی الیاف است
• E f {\displaystyle E_{f}} ویژگی مادهٔ الیاف است
• E m {\displaystyle E_{m}} ویژگی مادهٔ ماتریس است
در مورد مدول الاستیک، این رابطه به عنوان کران بالای مدول شناخته می شود و متناظر بارگذاری موازی با الیاف است. عکس قانون مخلوط ها بیان می کند که در جهت عمود بر الیاف، مدول الاستیک کامپوزیت می تواند حداقل برابر با مقدار زیر باشد:
E c = ( f E f + 1 − f E m ) − 1
اگر ویژگی مورد مطالعه مدول الاستیک باشد، این مقدار کران پایین مدول نامیده می شود و مربوط به بارگذاری عرضی است. [ ۲]
ماده کامپوزیتی را فرض کنید که تحت تنش تک محوری σ ∞ است. اگر ماده بدون تغییر بماند، کرنش الیاف ( شکست در تجزیه ( پاسخ نامعتبر MathML همراه SVG یا PNG جایگزین ( توصیه شده برای مرورگرهای مدرن و ابزارهای کمکی ) ( " Math extension cannot connect to Restbase. " ) از سرور " http://localhost:6011/fa. wikipedia. org/v1/" : ) : {\displaystyle \epsilon_f } ) باید برابر کرنش ماتریس ( ϵ m ) باشد. قانون هوک برای تنش تک محوری عبارتست از:
که در آن، σ f ، E f ، σ m و E m به ترتیب نشان دهندهٔ تنش و مدول الاستیک الیاف و ماتریس هستند. با توجه به این که تنش نیرو بر واحد سطح است، تعادل نیرو نتیجه زیر را بیان می کند: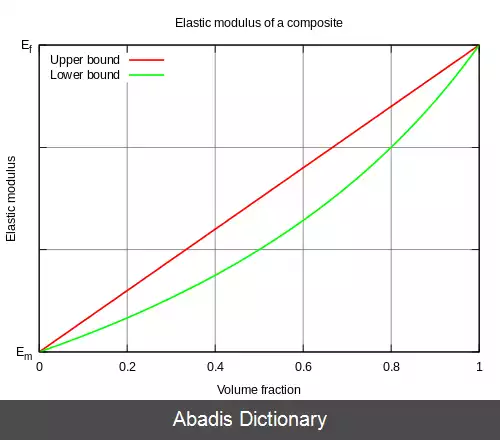
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبرای یک ویژگی ماده مثل E ( که اغلب مدول الاستیک[ ۱] است ) ، قانون مخلوط ها بیان می کند که اندازهٔ کلی ویژگی در جهت موازی با الیاف، می تواند حداکثر برابر مقدار زیر باشد:
E c = f E f + ( 1 − f ) E m
که در آن
• f = V f V f + V m {\displaystyle f={\frac {V_{f}}{V_{f}+V_{m}}}} کسر حجمی الیاف است
• E f {\displaystyle E_{f}} ویژگی مادهٔ الیاف است
• E m {\displaystyle E_{m}} ویژگی مادهٔ ماتریس است
در مورد مدول الاستیک، این رابطه به عنوان کران بالای مدول شناخته می شود و متناظر بارگذاری موازی با الیاف است. عکس قانون مخلوط ها بیان می کند که در جهت عمود بر الیاف، مدول الاستیک کامپوزیت می تواند حداقل برابر با مقدار زیر باشد:
E c = ( f E f + 1 − f E m ) − 1
اگر ویژگی مورد مطالعه مدول الاستیک باشد، این مقدار کران پایین مدول نامیده می شود و مربوط به بارگذاری عرضی است. [ ۲]
ماده کامپوزیتی را فرض کنید که تحت تنش تک محوری σ ∞ است. اگر ماده بدون تغییر بماند، کرنش الیاف ( شکست در تجزیه ( پاسخ نامعتبر MathML همراه SVG یا PNG جایگزین ( توصیه شده برای مرورگرهای مدرن و ابزارهای کمکی ) ( " Math extension cannot connect to Restbase. " ) از سرور " http://localhost:6011/fa. wikipedia. org/v1/" : ) : {\displaystyle \epsilon_f } ) باید برابر کرنش ماتریس ( ϵ m ) باشد. قانون هوک برای تنش تک محوری عبارتست از:
که در آن، σ f ، E f ، σ m و E m به ترتیب نشان دهندهٔ تنش و مدول الاستیک الیاف و ماتریس هستند. با توجه به این که تنش نیرو بر واحد سطح است، تعادل نیرو نتیجه زیر را بیان می کند:

wiki: قانون مخلوط ها
