در مثلثات، قانون سینوس ها معادله ای است که میان طول ضلع هر مثلث دلخواه و زاویهٔ مقابل آن ضلع رابطه برقرار می کند؛ این قانون عبارت است از:
که a و b و c به ترتیب ضلع های مثلث و α و β و γ به ترتیب زاویه های مقابل به هر ضلع اند. هنگامی که دو زاویه و یک ضلع مثلث را داشته باشیم از قانون سینوس ها استفاده می کنیم تا طول ضلع های دیگر مثلث را بدست آوریم.
قانون کروی سینوس ها در قرن ۱۰ میلادی کشف شد. این قانون را بیشتر به ابومحمود حامدبن خضر خجندی، ابوالوفای بوزجانی، خواجه نصیر طوسی و ابونصر منصور[ ۱] نسبت می دهند.
الجیانی در قرن ۱۱ میلادی کتابی نوشت با عنوان «کتاب کمان های ناشناخته در کره» ( به انگلیسی: The book of unknown arcs of a sphere ) و در آن به معرفی کلی قانون سینوس ها پرداخت. [ ۲] پس از او در قرن ۱۳ میلادی خواجه نصیر الدین طوسی به بیان این قانون میان صفحه ها پرداخت. او در کتابی با عنوان انگلیسی On the Sector Figure قانون سینوس ها را برای صفحه ها و مثلث های کروی بیان کرد و برای قانونش اثبات هایی را ارائه کرد. [ ۳]
در ادامه روش استفاده از قانون سینوس ها برای حل یک مسئله گفته شده است.
اگر فرض کنیم: ضلع های a = 20 و c = 24 و زاویهٔ C = 40° باشد، با استفاده از قانون سینوس ها می توان نتیجه گرفت که:
اگر داشته باشیم:
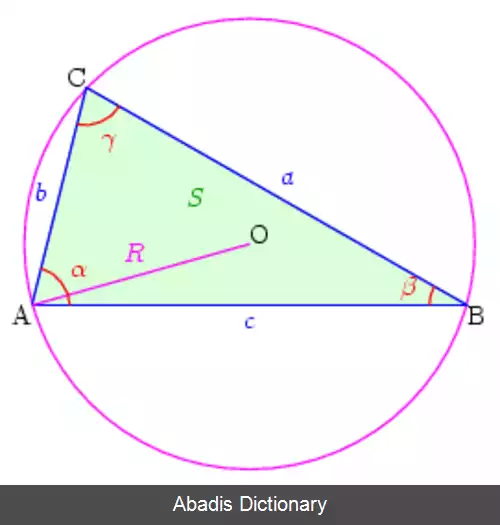
مقدار تک تک کسرهایی که در قانون سینوس ها نوشته می شود برابر است با قطر دایرهٔ محیطی مثلث می توان نشان داد که این مقدار خود برابر است با:
که در آن S مساحت مثلث است و p برابر با نصف محیط p = a + b + c 2 می باشد. همچنین رابطهٔ S = p ( p − a ) ( p − b ) ( p − c ) فرمول هرون بود که از آن در بالا استفاده شد.
وقتی از قانون سینوس ها استفاده می کنیم تا زاویه های یک مثلث را بدست آوریم، حالت هایی وجود دارند که ابهام برانگیزند و ما به جای یک جواب به دو جواب ( دو مثلث ) می رسیم.
اگر ABC یک مثلث دلخواه باشد اگر شرایط زیر اتفاق افتد:
• اطلاعات ما دربارهٔ مثلث تنها زاویهٔ A و ضلع های a و b باشد.
• زاویهٔ A یک زاویهٔ تند باشد ( کوچکتر از ۹۰ درجه ) .
• ضلع a کوچکتر از ضلع b باشد ( a < b ) .
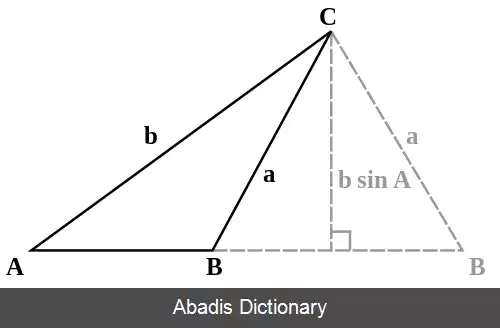
• ضلع a بزرگتر از ارتفاع مثلث راست گوشه با زاویهٔ A و وتر b باشد ( a> b sin A ) .
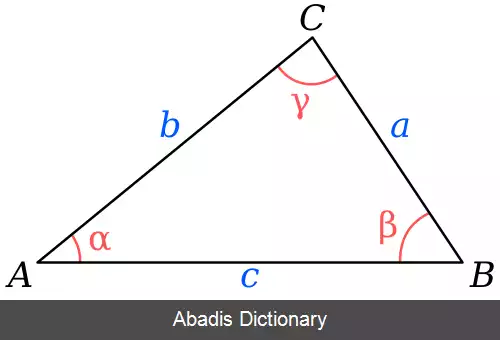


این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفکه a و b و c به ترتیب ضلع های مثلث و α و β و γ به ترتیب زاویه های مقابل به هر ضلع اند. هنگامی که دو زاویه و یک ضلع مثلث را داشته باشیم از قانون سینوس ها استفاده می کنیم تا طول ضلع های دیگر مثلث را بدست آوریم.
قانون کروی سینوس ها در قرن ۱۰ میلادی کشف شد. این قانون را بیشتر به ابومحمود حامدبن خضر خجندی، ابوالوفای بوزجانی، خواجه نصیر طوسی و ابونصر منصور[ ۱] نسبت می دهند.
الجیانی در قرن ۱۱ میلادی کتابی نوشت با عنوان «کتاب کمان های ناشناخته در کره» ( به انگلیسی: The book of unknown arcs of a sphere ) و در آن به معرفی کلی قانون سینوس ها پرداخت. [ ۲] پس از او در قرن ۱۳ میلادی خواجه نصیر الدین طوسی به بیان این قانون میان صفحه ها پرداخت. او در کتابی با عنوان انگلیسی On the Sector Figure قانون سینوس ها را برای صفحه ها و مثلث های کروی بیان کرد و برای قانونش اثبات هایی را ارائه کرد. [ ۳]
در ادامه روش استفاده از قانون سینوس ها برای حل یک مسئله گفته شده است.
اگر فرض کنیم: ضلع های a = 20 و c = 24 و زاویهٔ C = 40° باشد، با استفاده از قانون سینوس ها می توان نتیجه گرفت که:
اگر داشته باشیم:
مقدار تک تک کسرهایی که در قانون سینوس ها نوشته می شود برابر است با قطر دایرهٔ محیطی مثلث می توان نشان داد که این مقدار خود برابر است با:
که در آن S مساحت مثلث است و p برابر با نصف محیط p = a + b + c 2 می باشد. همچنین رابطهٔ S = p ( p − a ) ( p − b ) ( p − c ) فرمول هرون بود که از آن در بالا استفاده شد.
وقتی از قانون سینوس ها استفاده می کنیم تا زاویه های یک مثلث را بدست آوریم، حالت هایی وجود دارند که ابهام برانگیزند و ما به جای یک جواب به دو جواب ( دو مثلث ) می رسیم.
اگر ABC یک مثلث دلخواه باشد اگر شرایط زیر اتفاق افتد:
• اطلاعات ما دربارهٔ مثلث تنها زاویهٔ A و ضلع های a و b باشد.
• زاویهٔ A یک زاویهٔ تند باشد ( کوچکتر از ۹۰ درجه ) .
• ضلع a کوچکتر از ضلع b باشد ( a < b ) .
• ضلع a بزرگتر از ارتفاع مثلث راست گوشه با زاویهٔ A و وتر b باشد ( a> b sin A ) .






wiki: قانون سینوس ها
