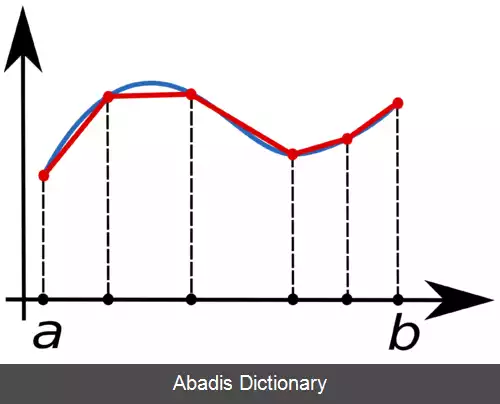
در آنالیز عددی، قانون ذوزنقه راهی برای محاسبهٔ تقریبی انتگرال معیّن است. قانون ذوزنقه از تقریب خطّی استفاده می کند. همان طور که در شکل می بینید بدین صورت است که می توان نمودار تابع را با تقریب خطی به یک سری ذوزنقه تبدیل کرد و سپس با محاسبهٔ مجموع مساحت های آن ها انتگرال تابع را به صورت حدّی به دست آورد.
برای محاسبه انتگرال تابعی که یکنواخت است، یک N در نظر گرفته و از بازهٔ کوچک تر شروع کرده و به اندازه N به بازهٔ اولیّه اضافه کرده تا به بازهٔ بزرگ تر برسیم که در واقع به این صورت می شود:
a = x 1 < x 2 < . . . < x N + 1 = b
و سپس، این x ها ارتفاع ذوزنقه می شود و با قرار دادنِ x ها در تابع، قاعدهٔ کوچک و بزرگ را به دست می آوریم و با استفاده از فرمول مساحت ذوزنقه، مساحت ذوزنقه را به دست آورده و جمع کرده و در نتیجه انتگرال را به دست می آوریم.
برای شبکه هایی که غیر یک نواخت است. از فرمول زیر استفاده می شود.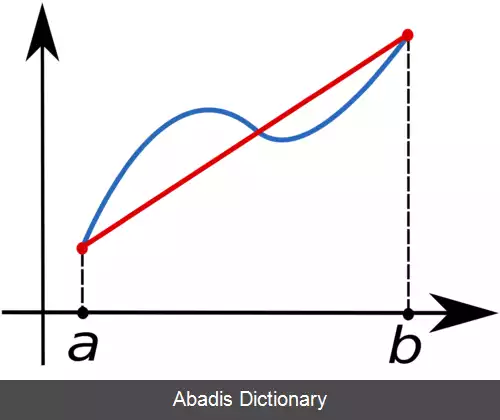
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبرای محاسبه انتگرال تابعی که یکنواخت است، یک N در نظر گرفته و از بازهٔ کوچک تر شروع کرده و به اندازه N به بازهٔ اولیّه اضافه کرده تا به بازهٔ بزرگ تر برسیم که در واقع به این صورت می شود:
a = x 1 < x 2 < . . . < x N + 1 = b
و سپس، این x ها ارتفاع ذوزنقه می شود و با قرار دادنِ x ها در تابع، قاعدهٔ کوچک و بزرگ را به دست می آوریم و با استفاده از فرمول مساحت ذوزنقه، مساحت ذوزنقه را به دست آورده و جمع کرده و در نتیجه انتگرال را به دست می آوریم.
برای شبکه هایی که غیر یک نواخت است. از فرمول زیر استفاده می شود.


wiki: قانون ذوزنقه
