قانون بِنفورد ( به انگلیسی: Benford's law ) یا قانون رقم اول می گوید که در فهرست عددهایی که در بسیاری از ( البته نه همهٔ ) پدیده های زندگی واقعی رخ می دهند، رقم اول عددها به طور خاص و غیریکنواختی توزیع می شود. بر طبق این قانون، تقریباً در یک سوم موارد رقم نخست ۱ است، و عددهای بزرگ تر در رقم نخست به ترتیب با بسامد کمتری رخ می دهند، و عدد ۹ کمتر از یک بار در هر بیست عدد ظاهر می شود.
علیرغم اینکه توزیع اعداد یا پدیده های طبیعی معمولا از توزیع نرمال تبعیت می کنند رقم اول این اعداد از قانون بنفورد تبعیت می کنند. به بیان دیگر می توان گفت که قانون بنفورد نوع دیگری از نمایش توزیع اعداد است که در آن اگر مجموعه اعدادی که رقم اول آنها ۱ و ۲ و ۳ و… است را کنار یکدیگر بگذاریم کل مجموعه را نمایش داده ایم. [ ۱] هرگاه که خود عددها به طور لگاریتمی توزیع شده باشند، این توزیع رقم های نخست منطقی خواهد بود. بنابر دلایلی، عددهایی که در سنجش های واقعی ثبت می شوند، معمولاً توزیع لگاریتمی دارند.
این قانون به نام فرانک بنفورد فیزیکدان نامیده شده است، هرچند که پیش از آن سیمون نیوکام در سال ۱۸۸۱ آن را بیان کرده بود.
اگر چه قانون بنفورد قطعاً به بسیاری از مجموعه داده ها اعمال می شود، توضیح علمی آن[ ۲] اخیراً و در سال ۱۹۹۸ توسط هیل، ریاضیدان، با استفاده از قضایای حد مرکزی - گونه داده شده است. [ ۳] در حقیقت تا پیش از سال ۱۹۹۶ هیچ کس نتوانست علت قانون بنفورد را به درستی توضیح دهد. سرانجام تئودور هیل ( T. Hill ) ثابت کرد که این قانون در سراسر جهان و حتی در دیگر دستگاه های شمارش مثل مبنای ۸ نیز صدق می کند. امروزه این قانون در حسابرسی های قانونی به شکل گسترده ای مورد استفاده قرار می گیرد، چرا که اگر حساب ها با قانون بنفورد مطابقت نداشته باشند به این معنی خواهد بود که حساب ها و اعداد به احتمال فراوان جعلی هستند. [ ۴] در کل قانون بنفورد یکی از بنیان های روش های کشف تقلب و کلاه برداری است. [ ۵]
این قانون به ظاهر عجیب در بسیاری از داده ها برقرار است، مثلاً در صورتحساب های برق، شمارهٔ خیابان ها، قیمت سهام، مقدار جمعیت، آمار مرگ ومیر، طول رودخانه ها، ثابت های فیزیک و ریاضیات، و فرایندهایی که از توزیع توانی پیروی می کنند ( که در طبیعت بسیار فراوانند ) . این قانون مستقل از پایه ای که عددها در آن بیان می شوند برقرار است، هرچند که احتمال تکرار عددها در هر پایه متفاوت از پایه های دیگر است. بین آماردانان و دانشمندان علوم سیاسی در مورد اعمال پذیری قانون بنفورد به داده های انتخاباتی اختلاف نظر وجود دارد. برخی مانند والتر میبین، [ ۶] استاد آمار و علوم سیاسی دانشگاه میشیگان معتقدند که رقم دوم داده ها از توزیع بنفورد پیروی می کند، [ ۷] در حالی که گزارش مرکز کارتر[ ۸] این دیدگاه را رد می کند.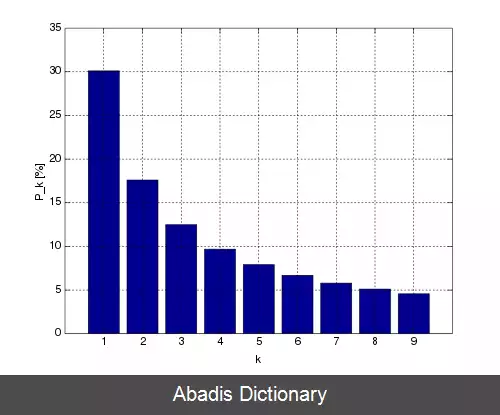

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفعلیرغم اینکه توزیع اعداد یا پدیده های طبیعی معمولا از توزیع نرمال تبعیت می کنند رقم اول این اعداد از قانون بنفورد تبعیت می کنند. به بیان دیگر می توان گفت که قانون بنفورد نوع دیگری از نمایش توزیع اعداد است که در آن اگر مجموعه اعدادی که رقم اول آنها ۱ و ۲ و ۳ و… است را کنار یکدیگر بگذاریم کل مجموعه را نمایش داده ایم. [ ۱] هرگاه که خود عددها به طور لگاریتمی توزیع شده باشند، این توزیع رقم های نخست منطقی خواهد بود. بنابر دلایلی، عددهایی که در سنجش های واقعی ثبت می شوند، معمولاً توزیع لگاریتمی دارند.
این قانون به نام فرانک بنفورد فیزیکدان نامیده شده است، هرچند که پیش از آن سیمون نیوکام در سال ۱۸۸۱ آن را بیان کرده بود.
اگر چه قانون بنفورد قطعاً به بسیاری از مجموعه داده ها اعمال می شود، توضیح علمی آن[ ۲] اخیراً و در سال ۱۹۹۸ توسط هیل، ریاضیدان، با استفاده از قضایای حد مرکزی - گونه داده شده است. [ ۳] در حقیقت تا پیش از سال ۱۹۹۶ هیچ کس نتوانست علت قانون بنفورد را به درستی توضیح دهد. سرانجام تئودور هیل ( T. Hill ) ثابت کرد که این قانون در سراسر جهان و حتی در دیگر دستگاه های شمارش مثل مبنای ۸ نیز صدق می کند. امروزه این قانون در حسابرسی های قانونی به شکل گسترده ای مورد استفاده قرار می گیرد، چرا که اگر حساب ها با قانون بنفورد مطابقت نداشته باشند به این معنی خواهد بود که حساب ها و اعداد به احتمال فراوان جعلی هستند. [ ۴] در کل قانون بنفورد یکی از بنیان های روش های کشف تقلب و کلاه برداری است. [ ۵]
این قانون به ظاهر عجیب در بسیاری از داده ها برقرار است، مثلاً در صورتحساب های برق، شمارهٔ خیابان ها، قیمت سهام، مقدار جمعیت، آمار مرگ ومیر، طول رودخانه ها، ثابت های فیزیک و ریاضیات، و فرایندهایی که از توزیع توانی پیروی می کنند ( که در طبیعت بسیار فراوانند ) . این قانون مستقل از پایه ای که عددها در آن بیان می شوند برقرار است، هرچند که احتمال تکرار عددها در هر پایه متفاوت از پایه های دیگر است. بین آماردانان و دانشمندان علوم سیاسی در مورد اعمال پذیری قانون بنفورد به داده های انتخاباتی اختلاف نظر وجود دارد. برخی مانند والتر میبین، [ ۶] استاد آمار و علوم سیاسی دانشگاه میشیگان معتقدند که رقم دوم داده ها از توزیع بنفورد پیروی می کند، [ ۷] در حالی که گزارش مرکز کارتر[ ۸] این دیدگاه را رد می کند.


wiki: قانون بنفورد
