در فیزیک قانون براگ نتایج آزمایش هایی است که در آن پرتو ایکس یا نوترون به سطح بلورین تابیده می شد که برای اولین بار توسط فیزیکدان ویلیام لارنس براگ بررسی شد[ ۱] که آزمایش هایش در سال ۱۹۱۱ و در دانشگاه کمبریج انجام شد. به طور ساده هنگام تابانیدن پرتوهایی مانند پرتو ایکس یا نوترون به سطوح بلورین بازتابش هایی انجام می گیرد که به این بازتاب ها پراش یا فرانژ گویند، که به همین دلیل براگ جایزه نوبل فیزیک را در سال ۱۹۱۵ به دست آورد سطوح بلورینی که او بررسی کرده بود عبارتند از NaCl، ZnS، و الماس.
قانون براگ براین اساس است که پرتوهای با طول موج مشخص و با زاویه مشخص به جسم بلورین تابانده می شود و با برخورد به اتم های مختلف جسم با تأخیر فازهای مختلف باز تابش هایی ایجاد می شود. این پرتوهای باز تابش شده در زاویه تتا با توجه به تأخیر فازهای مختلفشان حداکثر مقدار برهمکنشی را خواهند داشت. زاویه تتا وابسته به فاصله صفحه های کریستالی ویا فاصله اتمی آن ها می باشد با این روش می توان با توجه به زاویه حداکثر بازتابش پرتو انعکاس یافته از شبکه بلورین فاصله اتم جسم ویا فاصله صفحات کریستالی را بدست آورد. از طرفی می توان با مشخص بودن فاصله صفحات کریستالی جسم، زاویه تابش و زاویه حداکثر باز تابش طول موج تابش الکترومغناطیسی را بدست آورد. که از فرمول زیر تبعیت می کند
که
• n مرتبه بازتاب است و می تواند اعداد صحیح کوچکی باشد ( تعداد صفحه های کریستالی ) ،
• λ طول موج پرتو ایکس است که الکترون یا نوترون را جابجا نموده است،
• d فضای خالی میان اتمهاست و
• θ زاویه ای که پرتوهای بازتابیده شده بیشترین دامنه را دارند با راستای تابش پرتو های اولیه.
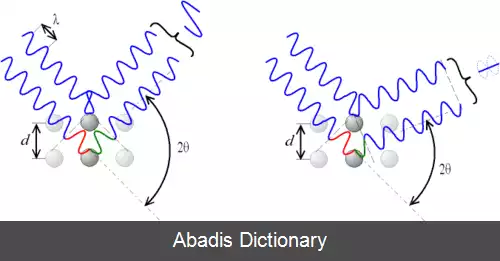
According to the ۲θ deviation, the phase shift causes constructive ( left figure ) or destructive ( right figure ) interferences
حرکت پروتون ها و نوترون ها و الکترون ها وابسته است به طول موج دوبروی آن ها.
برای بدست آوردن فضای میان اتمها می توان از حجم اتم ها چشم پوشید و آن را به صورت زیر نوشت:
که در آن d فاصلهٔ میان اتم هاست nتعداد اتم ها و vحجم جامد بلورین است تعداد اتم ها را می توان به راحتی از فرمول زیر بدست آورد:
که در آن N A عدد آووگادرو، N تعداد مول اتم هاm٬جرم ماده وM جرم مولی است. [ ۴]
یک پرتو تکرنگ هنگامی که به سطح بلورین منظمی که فاصله اتمهایش d هستند می تابد بعضی از پرتوها با زاویه تتا بازمی گردند به صورتی که: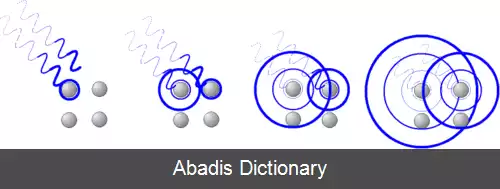
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفقانون براگ براین اساس است که پرتوهای با طول موج مشخص و با زاویه مشخص به جسم بلورین تابانده می شود و با برخورد به اتم های مختلف جسم با تأخیر فازهای مختلف باز تابش هایی ایجاد می شود. این پرتوهای باز تابش شده در زاویه تتا با توجه به تأخیر فازهای مختلفشان حداکثر مقدار برهمکنشی را خواهند داشت. زاویه تتا وابسته به فاصله صفحه های کریستالی ویا فاصله اتمی آن ها می باشد با این روش می توان با توجه به زاویه حداکثر بازتابش پرتو انعکاس یافته از شبکه بلورین فاصله اتم جسم ویا فاصله صفحات کریستالی را بدست آورد. از طرفی می توان با مشخص بودن فاصله صفحات کریستالی جسم، زاویه تابش و زاویه حداکثر باز تابش طول موج تابش الکترومغناطیسی را بدست آورد. که از فرمول زیر تبعیت می کند
که
• n مرتبه بازتاب است و می تواند اعداد صحیح کوچکی باشد ( تعداد صفحه های کریستالی ) ،
• λ طول موج پرتو ایکس است که الکترون یا نوترون را جابجا نموده است،
• d فضای خالی میان اتمهاست و
• θ زاویه ای که پرتوهای بازتابیده شده بیشترین دامنه را دارند با راستای تابش پرتو های اولیه.
According to the ۲θ deviation, the phase shift causes constructive ( left figure ) or destructive ( right figure ) interferences
حرکت پروتون ها و نوترون ها و الکترون ها وابسته است به طول موج دوبروی آن ها.
برای بدست آوردن فضای میان اتمها می توان از حجم اتم ها چشم پوشید و آن را به صورت زیر نوشت:
که در آن d فاصلهٔ میان اتم هاست nتعداد اتم ها و vحجم جامد بلورین است تعداد اتم ها را می توان به راحتی از فرمول زیر بدست آورد:
که در آن N A عدد آووگادرو، N تعداد مول اتم هاm٬جرم ماده وM جرم مولی است. [ ۴]
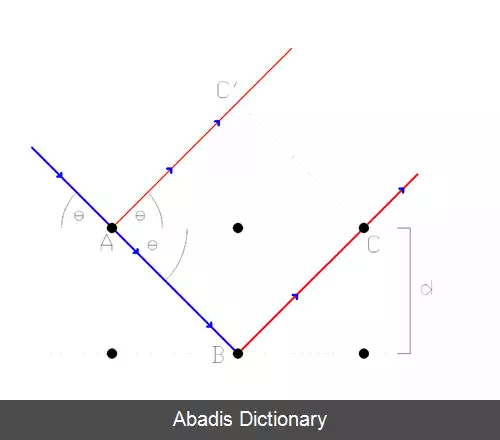
یک پرتو تکرنگ هنگامی که به سطح بلورین منظمی که فاصله اتمهایش d هستند می تابد بعضی از پرتوها با زاویه تتا بازمی گردند به صورتی که:



wiki: قانون براگ
