در نظریهٔ احتمالات، قانون اعداد بزرگ قضیه ای است که نتیجهٔ انجام یک آزمایش مشابه را برای چندین بار توصیف می کند. طبق این قانون، میانگین نتایج به دست آمده از تعداد زیادی آزمایش، باید به مقدار مورد انتظار ( امید ریاضی ) نزدیک باشد و با انجام آزمایش های بیشتر به مقدار مورد انتظار نزدیک تر می شود. [ ۱]
نکتهٔ مهم دربارهٔ قانون اعداد بزرگ این است که این قانون - همان طور که از نامش پیداست - تنها زمانی اعمال می شود که تعداد زیادی مشاهدات در نظر گرفته شود. هیچ اصلی وجود ندارد که تعداد کمی از مشاهدات با مقدار مورد انتظار منطبق شود. [ ۲]
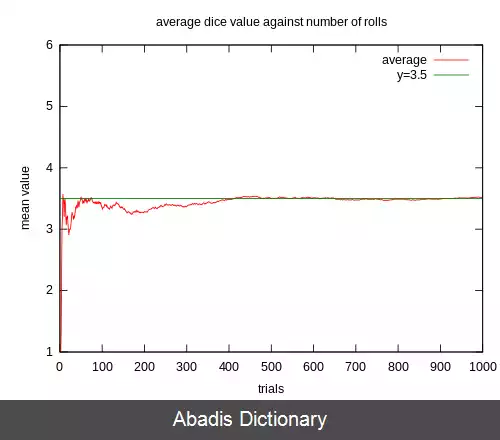
همچنین مهم است که توجه داشته باشید که قانون اعداد بزرگ فقط برای میانگین اعمال می شود. صورت ریاضی آن بدین شکل است: lim n → ∞ ∑ i = 1 n X i n − X ¯ = 0 فرمول های دیگری که مشابه به نظر می رسند قابل قبول نیستند. مانند انحراف معیارِ "نتایج نظری": ∑ i = 1 n X i − n × X ¯ این فرمول نه تنها با افزایش n به سمت صفر همگرا نمی شود، بلکه با افزایش n به یک مقدار ثابت میل خواهد کرد. [ ۳] مثال ها ۴۰۰ پیکسلبه عنوان یک مثال، وقتی یک تاس شش وجهی را یک بار بریزیم، یکی از عددهای ۱، ۲، ۳، ۴، ۵ یا ۶ به دست خواهد آمد. اگر این آزمایش را تکرار کنیم، هر دفعه یکی از این اعداد به دست می آیند و اگر تاس نااریب باشد، احتمال دیده شدن این اعداد با هم برابر است. در نتیجه، امید ریاضی عددی که با ریختن هر بار تاس به دست می آید، طبق این فرمول:
برابر با ۳٫۵ است. طبق قانون اعداد بزرگ، هرگاه آزمایش ریختن تاس را به دفعات زیاد تکرار کنیم، میانگین اعدادی که به دست می آید، تدریجاً به ۳٫۵ نزدیک خواهد شد. [ ۴]
به طور مثال می توان به آزمایش پرتاب سکه اشاره کرد. همان طور که می دانیم نتیجه این آزمایش توزیع برنولی دارد. اگر فقط یک بار آزمایش را انجام دهیم، احتمال رو آمدن سکه برابر ۱/۲ است، طبق قانون اعداد بزرگ اگر تعداد پرتاب ها زیاد باشد، نسبت تعداد رو آمدن ها به تعداد کل پرتاب ها به ۱/۲ میل می کند[ ۴] مشخص است که اختلاف تعداد روها و پشت ها با زیاد شدن تعداد آزمایش ها افزایش پیدا می کند. پس احتمال کوچک بودن اختلاف روها و پشت ها به سمت عدد صفر میل می کند. هم چنین می توان نتیجه گرفت که نسبت اختلاف روها و پشت ها به تعداد کل پرتاب ها نیز به سمت صفر می روند. از این حقیقت در می یابیم که با وجود رشد اختلاف بین تعداد روها و پشت ها در انجام این آزمایش به دفعات زیاد، سرعت این رشد از سرعت افزایش تعداد کل پرتاب ها کم تر است. [ ۴]

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفنکتهٔ مهم دربارهٔ قانون اعداد بزرگ این است که این قانون - همان طور که از نامش پیداست - تنها زمانی اعمال می شود که تعداد زیادی مشاهدات در نظر گرفته شود. هیچ اصلی وجود ندارد که تعداد کمی از مشاهدات با مقدار مورد انتظار منطبق شود. [ ۲]
همچنین مهم است که توجه داشته باشید که قانون اعداد بزرگ فقط برای میانگین اعمال می شود. صورت ریاضی آن بدین شکل است: lim n → ∞ ∑ i = 1 n X i n − X ¯ = 0 فرمول های دیگری که مشابه به نظر می رسند قابل قبول نیستند. مانند انحراف معیارِ "نتایج نظری": ∑ i = 1 n X i − n × X ¯ این فرمول نه تنها با افزایش n به سمت صفر همگرا نمی شود، بلکه با افزایش n به یک مقدار ثابت میل خواهد کرد. [ ۳] مثال ها ۴۰۰ پیکسلبه عنوان یک مثال، وقتی یک تاس شش وجهی را یک بار بریزیم، یکی از عددهای ۱، ۲، ۳، ۴، ۵ یا ۶ به دست خواهد آمد. اگر این آزمایش را تکرار کنیم، هر دفعه یکی از این اعداد به دست می آیند و اگر تاس نااریب باشد، احتمال دیده شدن این اعداد با هم برابر است. در نتیجه، امید ریاضی عددی که با ریختن هر بار تاس به دست می آید، طبق این فرمول:
برابر با ۳٫۵ است. طبق قانون اعداد بزرگ، هرگاه آزمایش ریختن تاس را به دفعات زیاد تکرار کنیم، میانگین اعدادی که به دست می آید، تدریجاً به ۳٫۵ نزدیک خواهد شد. [ ۴]
به طور مثال می توان به آزمایش پرتاب سکه اشاره کرد. همان طور که می دانیم نتیجه این آزمایش توزیع برنولی دارد. اگر فقط یک بار آزمایش را انجام دهیم، احتمال رو آمدن سکه برابر ۱/۲ است، طبق قانون اعداد بزرگ اگر تعداد پرتاب ها زیاد باشد، نسبت تعداد رو آمدن ها به تعداد کل پرتاب ها به ۱/۲ میل می کند[ ۴] مشخص است که اختلاف تعداد روها و پشت ها با زیاد شدن تعداد آزمایش ها افزایش پیدا می کند. پس احتمال کوچک بودن اختلاف روها و پشت ها به سمت عدد صفر میل می کند. هم چنین می توان نتیجه گرفت که نسبت اختلاف روها و پشت ها به تعداد کل پرتاب ها نیز به سمت صفر می روند. از این حقیقت در می یابیم که با وجود رشد اختلاف بین تعداد روها و پشت ها در انجام این آزمایش به دفعات زیاد، سرعت این رشد از سرعت افزایش تعداد کل پرتاب ها کم تر است. [ ۴]




wiki: قانون اعداد بزرگ
