قاعدهٔ هوپیتال یا لوپیتال ( به فرانسوی: L'Hôpital ) ( فرانسوی: ) در حساب، روشی است که با استفاده از آن می توان حد تابع را، در صورت وجود، در نقطه ای که مقدار آن 0 0 است بدست آورد. در واقع برای رفع ابهام ( 0 0 ) از این قاعده بهره می گیرند.
یوهان برنولی قراردادی با گیوم دو لوپیتال امضا کرد که به موجب آن می بایست کشفیات خود در ریاضیات را برای او بفرستد. نتیجه این شد که مهم ترین سهم برنولی در ریاضیات امروزه به نام قاعده هاپیتال و با تلفظ فرانسوی آن: قاعده لوپیتال نامیده می شود. [ نیازمند منبع]
فرض کنید تابع h یک تابع کسری باشد؛ به طوری که صورت این کسر برابر تابع f و مخرج آن برابر تابع g باشد، اگر حد توابع f و g ، صفر یا بی نهایت شود ( یعنی حد تابع h برابر 0 0 یا ∞ ∞ باشد ) ، می توان برای رفع ابهام، از صورت ( f ) و از مخرج ( g ) به طور جداگانه مشتق گرفته و هر کدام را در جای خود قرار دهیم و سپس حد تابع جدید را در نقطه مدنظر محاسبه کنیم:
اگر
یا
lim x → c f ( x ) = lim x → c g ( x ) = ± ∞
آنگاه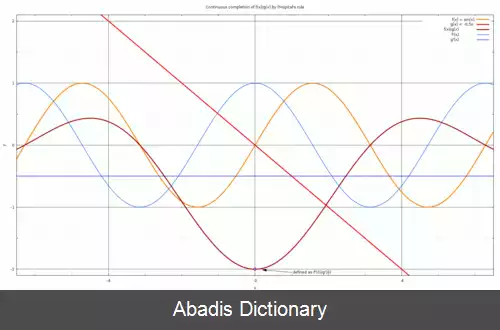
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیوهان برنولی قراردادی با گیوم دو لوپیتال امضا کرد که به موجب آن می بایست کشفیات خود در ریاضیات را برای او بفرستد. نتیجه این شد که مهم ترین سهم برنولی در ریاضیات امروزه به نام قاعده هاپیتال و با تلفظ فرانسوی آن: قاعده لوپیتال نامیده می شود. [ نیازمند منبع]
فرض کنید تابع h یک تابع کسری باشد؛ به طوری که صورت این کسر برابر تابع f و مخرج آن برابر تابع g باشد، اگر حد توابع f و g ، صفر یا بی نهایت شود ( یعنی حد تابع h برابر 0 0 یا ∞ ∞ باشد ) ، می توان برای رفع ابهام، از صورت ( f ) و از مخرج ( g ) به طور جداگانه مشتق گرفته و هر کدام را در جای خود قرار دهیم و سپس حد تابع جدید را در نقطه مدنظر محاسبه کنیم:
اگر
یا
lim x → c f ( x ) = lim x → c g ( x ) = ± ∞
آنگاه

wiki: قاعده هوپیتال
