در علم محاسبات عددی روشی برای بدست آوردن عددی انتگرال ها وجود دارد که توسط توماس سیمپسون مورد استفاده قرار گرفته است و به همین دلیل به این روش قاعده سیمپسون می گویند. در این قانون با استفاده از n بار استفاده از قانون ذوزنقه برای بدست آوردن مساحت زیر نمودار فرمولی برای مساحت زیر نمودار بدست میاورد که دقیقتر از روش ذوزنقه است. در این قانون با تقسیم کردن نمودار به بخش های کوچک تر مساحت زیر نمودار را بدست میاورد ( با تقسیم به n+1 بخش که n عددی زوج است ) .
البته حدود صد سال پیش از سیمپسون فردی به نام یوهانس کپلر از این فرمول استفاده کرده بود به همین دلیل گاهی به این روش قانون کپلر هم گفته می شود.
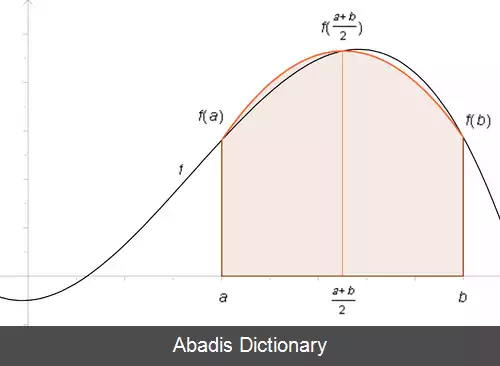
اگر اندازهٔ بازهٔ مورد انتگرال کوچک باشد، قاعده سیمپسون برای n = ۲ یک جواب نسبتاً دقیق از جواب انتگرال خواهد بود. اما اگر تابع ما پیوستگی نداشته باشد یا اندازهٔ بازهٔ مورد انتگرال بزرگ باشد یا تابع ما دارای مشتق های ناپیوسته باشد، در هر یک از این موارد قاعده سیمپسون برای n = ۲ جوابی دقیق ارائه نمی دهد. در این صورت می توان بازه را به n > 2 بخش تقسیم کرد و در هر یک از این بخش ها از قاعده سیمپسون استفاده کرد؛ که در این صورت به آن تعمیم قاعده سیمپسون گفته می شود. فرض کنید بازهٔ انتگرال به n بخش تقسیم شده است و همچنین n را عددی زوج در نظر بگیرید در این صورت طبق قاعده سیمپسون داریم
∫ a b f ( x ) d x ≈ h 3 ∑ j = 1 n / 2 = h 3
که در این فرمول x j = a + j h برای j = 0 , 1 , . . . , n − 1 , n و در آن h = ( b − a ) / n
خطای تعمیم قاعده سیمپسون برابر است با[ ۱]
E r r o r = − h 4 180 ( b − a ) f ( 4 ) ( ξ )
که در آن ξ عددی بین a و b است و h = ( b − a ) / n طول هر گام است.
اگر چندجمله ای درجهٔ دو P ( x ) را به جای تابع f ( x ) در فرمول استفاده کنیم می توان با استفاده از درونیابی می توان این چندجمله ای را بدست آورد. [ ۲]
P ( x ) = f ( a ) ( x − m ) ( x − b ) ( a − m ) ( a − b ) + f ( m ) ( x − a ) ( x − b ) ( m − a ) ( m − b ) + f ( b ) ( x − a ) ( x − m ) ( b − a ) ( b − m ) با انتگرال گرفتن از دو طرف تساوی و استفاده از قانون لاگرانژ داریم:
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفالبته حدود صد سال پیش از سیمپسون فردی به نام یوهانس کپلر از این فرمول استفاده کرده بود به همین دلیل گاهی به این روش قانون کپلر هم گفته می شود.
اگر اندازهٔ بازهٔ مورد انتگرال کوچک باشد، قاعده سیمپسون برای n = ۲ یک جواب نسبتاً دقیق از جواب انتگرال خواهد بود. اما اگر تابع ما پیوستگی نداشته باشد یا اندازهٔ بازهٔ مورد انتگرال بزرگ باشد یا تابع ما دارای مشتق های ناپیوسته باشد، در هر یک از این موارد قاعده سیمپسون برای n = ۲ جوابی دقیق ارائه نمی دهد. در این صورت می توان بازه را به n > 2 بخش تقسیم کرد و در هر یک از این بخش ها از قاعده سیمپسون استفاده کرد؛ که در این صورت به آن تعمیم قاعده سیمپسون گفته می شود. فرض کنید بازهٔ انتگرال به n بخش تقسیم شده است و همچنین n را عددی زوج در نظر بگیرید در این صورت طبق قاعده سیمپسون داریم
∫ a b f ( x ) d x ≈ h 3 ∑ j = 1 n / 2 = h 3
که در این فرمول x j = a + j h برای j = 0 , 1 , . . . , n − 1 , n و در آن h = ( b − a ) / n
خطای تعمیم قاعده سیمپسون برابر است با[ ۱]
E r r o r = − h 4 180 ( b − a ) f ( 4 ) ( ξ )
که در آن ξ عددی بین a و b است و h = ( b − a ) / n طول هر گام است.
اگر چندجمله ای درجهٔ دو P ( x ) را به جای تابع f ( x ) در فرمول استفاده کنیم می توان با استفاده از درونیابی می توان این چندجمله ای را بدست آورد. [ ۲]
P ( x ) = f ( a ) ( x − m ) ( x − b ) ( a − m ) ( a − b ) + f ( m ) ( x − a ) ( x − b ) ( m − a ) ( m − b ) + f ( b ) ( x − a ) ( x − m ) ( b − a ) ( b − m ) با انتگرال گرفتن از دو طرف تساوی و استفاده از قانون لاگرانژ داریم:



wiki: قاعده سیمپسون
