فرایند تولد مرگ ( زاد مرگ ) صورت خاصی از فرایند مارکف زمان گسسته است که در آن تغییر حالت ها تنها از دو نوع است:
• تولد: در این حالت مقدار وضعیت ۱ واحد افزایش می یابد.
• مرگ: در این حالت مقدار وضعیت ۱ واحد کاهش می یابد.
اسم مدل از کاربردهای معمول می آید٬مانند زمانی که استفاده از این مدل ها برای نشان دادن سایز فعلی جمعیت و مدلی از مرگ و تولد به معنای واقعی به کار می رود. فرایندهای زاد و مرگ کاربردهای زیادی در آمارنگاری مردم٬تئوری صف٬مهندسی کارائی٬علم امراض مسری یا در زیست شناسی دارد. این روش می تواند در کاربرد هائی نظیر مطالعهٔ تکامل باکتری ها٬تعداد مردم با وجود یک بیماری در جمعیت٬یا تعداد مشتری ها در یک صف سوپرمارکت استفاده شود.
هنگامی که تولد رخ می دهد فرایند از حالت n به n + 1 می رود. هنگامی که مرگ رخ می دهد فرایند از حالت n به حالت n − 1 می رود. این فرایند را می توان با نرخ تولد { λ i } i = 0 … ∞ و نرخ مرگ { μ i } i = 1 … ∞ مشخص نمود.
یک فرایند زاد - مرگ را یک فرایند تولد خالص می نامیم اگر در آن برای همهٔ i ≥ 0 داشته باشیم μ i = 0 .
یک فرایند زاد - مرگ را یک فرایند مرگ خالص می نامیم اگر در آن برای همهٔ i ≥ 0 داشته باشیم λ i = 0 .
فرایند پواسون ( همگن ) حالتی خاصی از فرایند زاد - مرگ خالص است که برای آن داشته باشیم λ i = λ .
مدل M/M/1 و مدل M/M/c که هر دو در تئوری صف استفاده شده اند، فرایند تولد مرگی هستند که برای توصیف مشتریان در صف نامحدود استفاده می شوند.
در تئوری صف فرایند تولد مرگ یکی از اساسی ترین مثال های مدل صف بندی M/M/C/K/ ∞ /FIFO/ ( در علامت گذاری کامل kandell ) است. این یک صف با ورود پواسون است که از یک جمعیت بینهایت که از C سرویس رسان با زمان سرویس توزیع نمائی با K مکان استفاده می کند. به رغم فرض جمعیت نامحدود، این مدل یک مدل خوب برای سیستم های مخابراتی متنوع است.
M/M/1 یک صف سرویس رسانی منفرد از اندازه بافر بی نهایت است. در محیط غیر تصادفی، فرایند تولد مرگ در مدل صف بندی تمایل دارد که با میانگین بلند مدت باشد٬بنابراین نرخ میانگین ورودها به صورت λ و متوسط زمان سرویس دهی به صورت 1 / μ می باشد. فرایند تولد و مرگ یک صف M/M/1 است زمانی که داشته باشیم: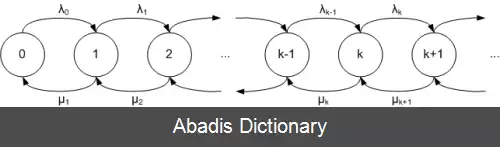
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف• تولد: در این حالت مقدار وضعیت ۱ واحد افزایش می یابد.
• مرگ: در این حالت مقدار وضعیت ۱ واحد کاهش می یابد.
اسم مدل از کاربردهای معمول می آید٬مانند زمانی که استفاده از این مدل ها برای نشان دادن سایز فعلی جمعیت و مدلی از مرگ و تولد به معنای واقعی به کار می رود. فرایندهای زاد و مرگ کاربردهای زیادی در آمارنگاری مردم٬تئوری صف٬مهندسی کارائی٬علم امراض مسری یا در زیست شناسی دارد. این روش می تواند در کاربرد هائی نظیر مطالعهٔ تکامل باکتری ها٬تعداد مردم با وجود یک بیماری در جمعیت٬یا تعداد مشتری ها در یک صف سوپرمارکت استفاده شود.
هنگامی که تولد رخ می دهد فرایند از حالت n به n + 1 می رود. هنگامی که مرگ رخ می دهد فرایند از حالت n به حالت n − 1 می رود. این فرایند را می توان با نرخ تولد { λ i } i = 0 … ∞ و نرخ مرگ { μ i } i = 1 … ∞ مشخص نمود.
یک فرایند زاد - مرگ را یک فرایند تولد خالص می نامیم اگر در آن برای همهٔ i ≥ 0 داشته باشیم μ i = 0 .
یک فرایند زاد - مرگ را یک فرایند مرگ خالص می نامیم اگر در آن برای همهٔ i ≥ 0 داشته باشیم λ i = 0 .
فرایند پواسون ( همگن ) حالتی خاصی از فرایند زاد - مرگ خالص است که برای آن داشته باشیم λ i = λ .
مدل M/M/1 و مدل M/M/c که هر دو در تئوری صف استفاده شده اند، فرایند تولد مرگی هستند که برای توصیف مشتریان در صف نامحدود استفاده می شوند.
در تئوری صف فرایند تولد مرگ یکی از اساسی ترین مثال های مدل صف بندی M/M/C/K/ ∞ /FIFO/ ( در علامت گذاری کامل kandell ) است. این یک صف با ورود پواسون است که از یک جمعیت بینهایت که از C سرویس رسان با زمان سرویس توزیع نمائی با K مکان استفاده می کند. به رغم فرض جمعیت نامحدود، این مدل یک مدل خوب برای سیستم های مخابراتی متنوع است.
M/M/1 یک صف سرویس رسانی منفرد از اندازه بافر بی نهایت است. در محیط غیر تصادفی، فرایند تولد مرگ در مدل صف بندی تمایل دارد که با میانگین بلند مدت باشد٬بنابراین نرخ میانگین ورودها به صورت λ و متوسط زمان سرویس دهی به صورت 1 / μ می باشد. فرایند تولد و مرگ یک صف M/M/1 است زمانی که داشته باشیم:

wiki: فرایند تولد مرگ
