در ریاضیات فرایند اورنشتاین - اولنبک ( برگرفته شده از نام لئونارد اورنشتاین و جرج اولنبک ) فرایند تصادفی است که به طور کلی سرعت توده ای از ذرات برونی تحت تأثیر اصطکاک را توصیف می کند. این فرایند، فرایند گاوس–مارکف ( فرایندی با مشخصات گوسی و مارکوف ) ایستا بوده و تنها فرایند غیرجزئی است که سه شرط فرایندهای گاوسی - مارکوف را ارضا کرده و تبدیلات خطی فضا و زمان را ممکن می سازد. [ ۱] در طول زمان این فرایند به میانگین طولانی مدت خود میل می کند: به این فرایندها، بازگشت به میانگین می گویند.
این فرایند را می توان به عنوان تبدیلی از قدم زدن تصادفی در زمان پیوسته، یا فرایند وینر دانست که در آن خواص به گونه ای تغییر کرده است که قدم زدن و بازگشت به سمت محل مرکزی تمایل داشته و هرچه فاصله از این مرکز بیشتر باشد، شدت تمایل نیز بیشتر خواهد شد. فرایند اورنستین - یولنبک را نیز می توان به عنوان آنالوگ پیوسته - زمان فرایند گسسته - زمان AR ( 1 ) در نظر گرفت.
فرایند اورنشتاین - یولنبک Xt تساوی دیفرانسیلی تصادفی زیر را ارضا می کند:
که در آن θ > 0 با μ و σ > 0 پارامترها بوده و W t نشان دهنده فرایند وینر است.
نمایش بالا را می توان به عنوان تعریف اصلی فرایند اورنستین - یولنبک دانست[ ۱] [ نیازمند منبع] و که به عنوان مدل واسیک نیز معرفی می گردد. [ ۲]
تابع دانسیته احتمال ) ƒ ( x, t فرایند اورنشتاین - اولنبک تساوی فوکر - پلانک را مرتفع می کند:
↑ ۱٫۰ ۱٫۱ ( ] ) ↑ Björk, Tomas ( 2009 ) . Arbitrage Theory in Continuous Time ( 3 ed. ) . Oxford University Press. pp. 375, 381. ISBN 978 - 0 - 19 - 957474 - 2.
• انواع قدم زنی تصادفی
• فرایندهای مارکف
• معادله های دیفرانسیل تصادفی
• همه مقاله های دارای عبارت های بدون منبع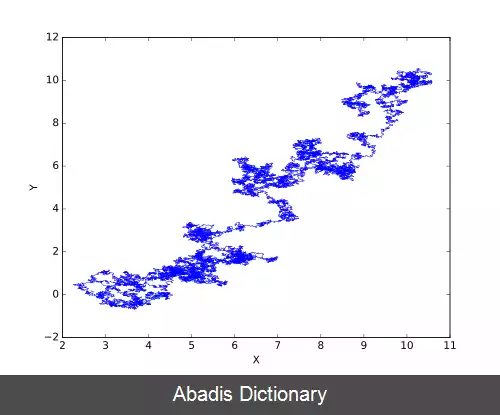
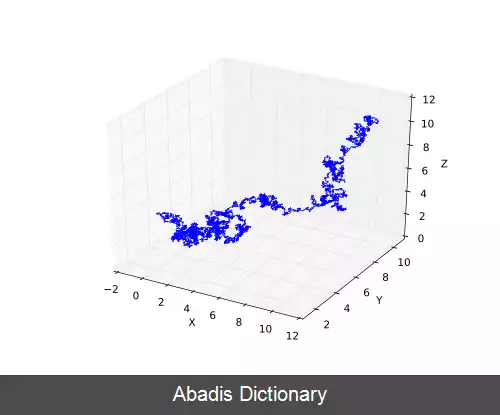
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین فرایند را می توان به عنوان تبدیلی از قدم زدن تصادفی در زمان پیوسته، یا فرایند وینر دانست که در آن خواص به گونه ای تغییر کرده است که قدم زدن و بازگشت به سمت محل مرکزی تمایل داشته و هرچه فاصله از این مرکز بیشتر باشد، شدت تمایل نیز بیشتر خواهد شد. فرایند اورنستین - یولنبک را نیز می توان به عنوان آنالوگ پیوسته - زمان فرایند گسسته - زمان AR ( 1 ) در نظر گرفت.
فرایند اورنشتاین - یولنبک Xt تساوی دیفرانسیلی تصادفی زیر را ارضا می کند:
که در آن θ > 0 با μ و σ > 0 پارامترها بوده و W t نشان دهنده فرایند وینر است.
نمایش بالا را می توان به عنوان تعریف اصلی فرایند اورنستین - یولنبک دانست[ ۱] [ نیازمند منبع] و که به عنوان مدل واسیک نیز معرفی می گردد. [ ۲]
تابع دانسیته احتمال ) ƒ ( x, t فرایند اورنشتاین - اولنبک تساوی فوکر - پلانک را مرتفع می کند:
↑ ۱٫۰ ۱٫۱ ( ] ) ↑ Björk, Tomas ( 2009 ) . Arbitrage Theory in Continuous Time ( 3 ed. ) . Oxford University Press. pp. 375, 381. ISBN 978 - 0 - 19 - 957474 - 2.
• انواع قدم زنی تصادفی
• فرایندهای مارکف
• معادله های دیفرانسیل تصادفی
• همه مقاله های دارای عبارت های بدون منبع


wiki: فرایند اورنستین یولنبک
