در زمان های گذشته، مردم تصور می کردند که تنها راه محاسبه مسافت، استفاده از روش های اقلیدسی است. با شروع قرن نوزدهم، ریاضیدانان روش هایی را کشف کردند که با روش پیشین تفاوت بسیاری داشت. در آن زمان ریاضیدانان شروع به خلق هندسه های غیراقلیدسی کردند. هرمان مینکوفسکی، ریاضیدان آلمانی، کسی است که مفهوم «هندسه تاکسی» و روش های متعدد دیگری برای اندازه گیری فاصله را معرفی کرد. علت اینکه دانشمندان در تلاش برای کشف روش های غیراقلیدسی اندازه گیری فاصله بودند، به این موضوع برمی گردد که کل ساختار فضا - زمان از هندسه اقلیدسی تبعیت نمی کند و جهان به صورت مجموعه ای از فواصل گسسته تعریف می شود. حاصل تلاش مینکوفسکی و دانشمندان دیگر بود که اینشتین را به سوی تئوری معروف نسبیت اش سوق داد.
روش هندسه تاکسی، فاصله دو نقطه را به جای کوتاه ترین خطی که آن ها را بهم متصل می کند، به صورت خطوط افقی و عمودی که آن دو نقطه را بهم می رساند نشان می دهد. فاصله بین دو ساختمان اگر سوار بر یک تاکسی هستید مجموع مسیرهای افقی و عمودی ای است که تاکسی از مبدأ تا مقصد می پیماید. در این روش به جای خطوط مورب، مجموع طول خطوط عمودی و افقی فاصله دو نقطه را تعیین می کند.
این روش به نام های دیگری چون فاصله مستطیل، طول نرمال، روش مارگونه، فاصله بلوک های شهر و فاصله منهتن یا طول منهتن نیز شناخته می شود. نام " فاصله منهتن، اشاره به ساختار شبکه گونهٔ خیابان ها و تقاطع های منطقه منهتن در شهر نیویورک دارد.
این مفهوم از قرن هجدهم در تحلیل های رگرسیون و لسو ( LASSO ) مورد استفاده بوده است.
فاصله منهتن، d 1 ، بین دو بردار p و q در یک فضای n بعدی به شکل زیر محاسبه می شود:
d 1 ( p , q ) = ‖ p − q ‖ 1 = ∑ i = 1 n | p i − q i | ,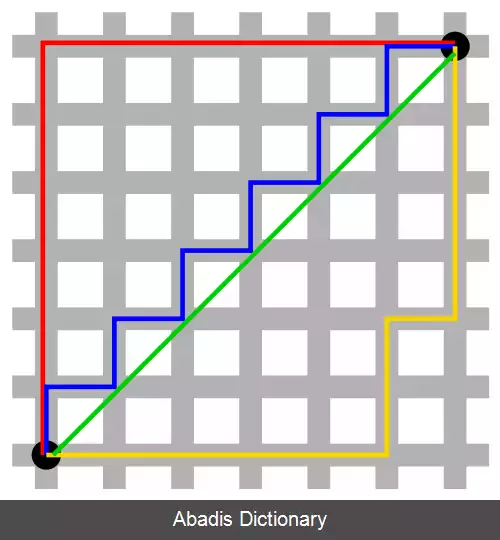
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفروش هندسه تاکسی، فاصله دو نقطه را به جای کوتاه ترین خطی که آن ها را بهم متصل می کند، به صورت خطوط افقی و عمودی که آن دو نقطه را بهم می رساند نشان می دهد. فاصله بین دو ساختمان اگر سوار بر یک تاکسی هستید مجموع مسیرهای افقی و عمودی ای است که تاکسی از مبدأ تا مقصد می پیماید. در این روش به جای خطوط مورب، مجموع طول خطوط عمودی و افقی فاصله دو نقطه را تعیین می کند.
این روش به نام های دیگری چون فاصله مستطیل، طول نرمال، روش مارگونه، فاصله بلوک های شهر و فاصله منهتن یا طول منهتن نیز شناخته می شود. نام " فاصله منهتن، اشاره به ساختار شبکه گونهٔ خیابان ها و تقاطع های منطقه منهتن در شهر نیویورک دارد.
این مفهوم از قرن هجدهم در تحلیل های رگرسیون و لسو ( LASSO ) مورد استفاده بوده است.
فاصله منهتن، d 1 ، بین دو بردار p و q در یک فضای n بعدی به شکل زیر محاسبه می شود:
d 1 ( p , q ) = ‖ p − q ‖ 1 = ∑ i = 1 n | p i − q i | ,

wiki: فاصله منهتن
