در ریاضیات، به خصوص در نظریه ترتیب، یک عنصر ماکسیمال ( Maximal Element ) از زیرمجموعه S از یک مجموعه مرتب جزئی ( poset ) ، عنصری از S است که از هیچ عنصر دیگری از S کوچکتر نباشد. تعریف عنصر مینیمال ( Minimal Element ) ، دوگان تعریف اخیر است: عنصری از S که از هیچ عنصر دیگر S بزرگتر نباشد.
مفاهیم عناصر ماکسیمال و مینیمال به ترتیب از بزرگترین و کوچکترین عنصر ( یا ماکسیمم و مینیمم ) ضعیف ترند. ماکسیمم زیرمجموعه S از یک مجموعه مرتب جزئی، عنصری از S است که از هر عنصر S بزرگتر مساوی بوه و مینیمم S نیز به صورت دوگان ماکسیمم تعریف می شود. درحالی که مجموعه مرتب جزئی حداکثر یک ماکسیمم و حداکثر یک مینیمم دارد، تعداد هرکدام از عناصر ماکسیمال و مینیمال ممکن است بیش از یکی باشند. [ ۱] [ ۲] مفاهیم عناصر ماکسیمال و ماکسیمم برای مجموعه های مرتب کلی یکی می شوند، همچنین مینیمال و مینیمم برای چنین مجموعه هایی یکی می شوند.
به عنوان مثال مجموعه زیر را در نظر بگیرید:
S = { { d , o } , { d , o , g } , { g , o , a , d } , { o , a , f } }
اگر ترتیب شمول ( زیرمجموعه بودن ) را بر روی آن در نظر بگیریم، عنصر { d , o } در مجموعه فوق مینیمال است، چرا که شامل هیچ مجموعه دیگری از S نیست. عنصر { g , o , a , d } در آن ماکسیمال است، چرا که هیچ مجموعه دیگری از S آن را دربر ندارد. عنصر { d , o , g } نه مینیمال است و نه ماکسیمال، در حالی که { o , a , f } هم ماکسیمال است و هم مینیمال. برهمین اساس مجموعه S هیچ ماکسیمم یا مینیممی ندارد.
لم زرن بیان می کند که هر مجموعه مرتب جزئی که هر زیرمجموعه مرتب کلی آن ( زنجیره ها ) دارای کران بالا باشد، شامل حداقل یک عنصر ماکسیمال است. این لم معادل با قضیه خوش - ترتیبی و اصل موضوع انتخاب است. [ ۳] لم زرن نتایج مهمی را در سایر شاخه های ریاضیات ایجاب می کند: قضیه هان - باناخ، قضیه کیرسزبراون، قضیه تیخونوف، وجود پایه همل برای هر فضای برداری و وجود بستار جبری برای هر میدان.
( P , ≤ ) مجموعه جزئاً مرتب و S ⊂ P . آنگاه m ∈ S است یک عضو بیشین S اگر
برای همه s ∈ S با m ≤ s قرار دهیم m = s .
تعریف عضو کمین با استفاده از ≤ به جای ≥ حاصل می شود.
عناصر بیشین لزوماً وجود ندارند.
به طور کلی ≤ فقط یک مرتب جزیی روی S است. اگر m یک عضو بیشین و s∈S باشد، احتمال اینکه نه s≤m و نه m≤s باشد، باقی می ماند. این، احتمال اینکه آنجا بسیاری ازعضوهای بیشین هست را باقی می گذارد.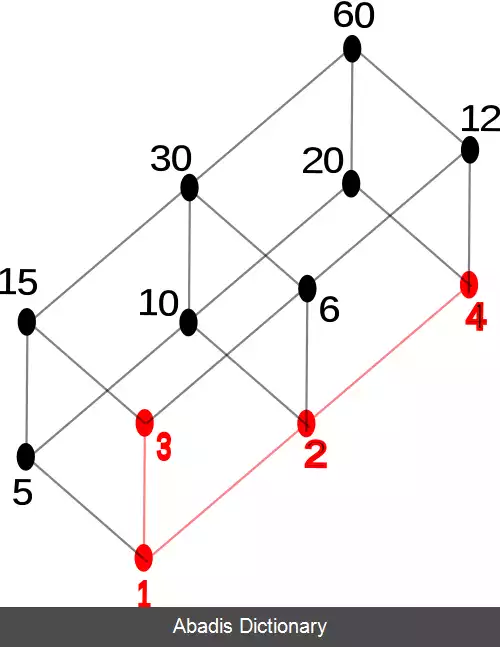
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمفاهیم عناصر ماکسیمال و مینیمال به ترتیب از بزرگترین و کوچکترین عنصر ( یا ماکسیمم و مینیمم ) ضعیف ترند. ماکسیمم زیرمجموعه S از یک مجموعه مرتب جزئی، عنصری از S است که از هر عنصر S بزرگتر مساوی بوه و مینیمم S نیز به صورت دوگان ماکسیمم تعریف می شود. درحالی که مجموعه مرتب جزئی حداکثر یک ماکسیمم و حداکثر یک مینیمم دارد، تعداد هرکدام از عناصر ماکسیمال و مینیمال ممکن است بیش از یکی باشند. [ ۱] [ ۲] مفاهیم عناصر ماکسیمال و ماکسیمم برای مجموعه های مرتب کلی یکی می شوند، همچنین مینیمال و مینیمم برای چنین مجموعه هایی یکی می شوند.
به عنوان مثال مجموعه زیر را در نظر بگیرید:
S = { { d , o } , { d , o , g } , { g , o , a , d } , { o , a , f } }
اگر ترتیب شمول ( زیرمجموعه بودن ) را بر روی آن در نظر بگیریم، عنصر { d , o } در مجموعه فوق مینیمال است، چرا که شامل هیچ مجموعه دیگری از S نیست. عنصر { g , o , a , d } در آن ماکسیمال است، چرا که هیچ مجموعه دیگری از S آن را دربر ندارد. عنصر { d , o , g } نه مینیمال است و نه ماکسیمال، در حالی که { o , a , f } هم ماکسیمال است و هم مینیمال. برهمین اساس مجموعه S هیچ ماکسیمم یا مینیممی ندارد.
لم زرن بیان می کند که هر مجموعه مرتب جزئی که هر زیرمجموعه مرتب کلی آن ( زنجیره ها ) دارای کران بالا باشد، شامل حداقل یک عنصر ماکسیمال است. این لم معادل با قضیه خوش - ترتیبی و اصل موضوع انتخاب است. [ ۳] لم زرن نتایج مهمی را در سایر شاخه های ریاضیات ایجاب می کند: قضیه هان - باناخ، قضیه کیرسزبراون، قضیه تیخونوف، وجود پایه همل برای هر فضای برداری و وجود بستار جبری برای هر میدان.
( P , ≤ ) مجموعه جزئاً مرتب و S ⊂ P . آنگاه m ∈ S است یک عضو بیشین S اگر
برای همه s ∈ S با m ≤ s قرار دهیم m = s .
تعریف عضو کمین با استفاده از ≤ به جای ≥ حاصل می شود.
عناصر بیشین لزوماً وجود ندارند.
به طور کلی ≤ فقط یک مرتب جزیی روی S است. اگر m یک عضو بیشین و s∈S باشد، احتمال اینکه نه s≤m و نه m≤s باشد، باقی می ماند. این، احتمال اینکه آنجا بسیاری ازعضوهای بیشین هست را باقی می گذارد.



wiki: عناصر ماکسیمال و مینیمال
