در نظریه گراف، عرض درختی یک گراف بدون جهت، عددی است که مربوط به آن گراف است. این عدد می تواند به طرق مختلفی تعریف شود: اندازهٔ بزرگ ترین راس در تجریهٔ درختی آن گراف، اندازهٔ بزرگ ترین خوشه در تکمیل وتری و . . . . مفهوم عرض درختی یک گراف، در ابتدا توسط Umberto Bertelé و Francesco Brioschi در سال ۱۹۷۲ معرفی شد. بعدها به صورت جدی توسط Neil Robertson و Paul Seymour در سال ۱۹۸۴ مجدداً معرفی گردید. برای تعریف عرض درختی یک گراف، ابتدا باید تجریهٔ درختی گراف را تعریف کنیم.
تجزیهٔ درختی گراف G = ( V , E ) ، درختی است مانند T با رئوس X 1 , X 2 , . . . , X n ( به این رئوس کیف یا bag می گویند ) که در آن هر X i یک زیرمجموعه ای از V است که شرایط زیر را ارضا کند:
• اجتماع تمامی X i {\displaystyle X_{i}} ها، مجموعهٔ V {\displaystyle V} باشد.
• تمامی رئوس ( کیف های ) درخت که شامل راس v ∈ V {\displaystyle v\in V} هستند، تشکیل یک زیردرخت هم بند بدهند.
• برای هر یال مانند ( u , v ) {\displaystyle ( u, v ) } در گراف G {\displaystyle G} ، حداقل یک راس ( کیف ) مانند X i {\displaystyle X_{i}} در درخت باشد که شامل هر دو راس u {\displaystyle u} و v {\displaystyle v} است.
تجزیهٔ درختی یک گراف، یکتا نیست. بدیهی ترین تجزیهٔ درختی، قراردادن تمامی رئوس گراف در یک کیف است که در این صورت هر گراف یک تجزیه با عرض n − 1 دارد؛ بنابراین برای هر گراف تجزیه های درختی متعددی وجود دارد. عرض درختی یک تجزیهٔ درختی، برابر است با سایز بزرگ ترین کیف آن منهای یک. عرض درختی یک گراف نیز که با t w ( G ) نمایش داده می شود، برابرست با کم ترین عرض درختی میان تمامی تجریه های درختی آن گراف.
مثال: در شکل زیر گراف G و یک تجزیهٔ درختی از آن را می بینید. عرض این تجزیهٔ درختی، ۲ می باشد.
مثال: عرض درختی تمام درخت ها برابر با یک است.
تجزیهٔ درختی ( X i | i ∈ I , T ( I , F ) ) با عرض k نرم می گوییم اگر:
• ∀ i | X i | = k + 1 {\displaystyle \forall i\quad |X_{i}|=k+1}
• ∀ i , j ∈ F | X i ⋂ X j | = k {\displaystyle \forall {i, j}\in F\quad |X_{i}\bigcap X_{j}|=k}
نکته: هر تجزیهٔ درختی را می توان به یک تجزیهٔ درختی نرم تبدیل کرد.
فرض کنید ( X i | i ∈ I , T ( I , F ) ) یک تجزیهٔ درختی برای گراف G = ( V , E ) باشد به طوری که عرض آن حداکثر k باشد. می خواهیم الگوریتمی از O ( k 2 4 k | V | ) ارائه دهیم تا بزرگ ترین مجموعهٔ مستقل این گراف را پیدا کنیم.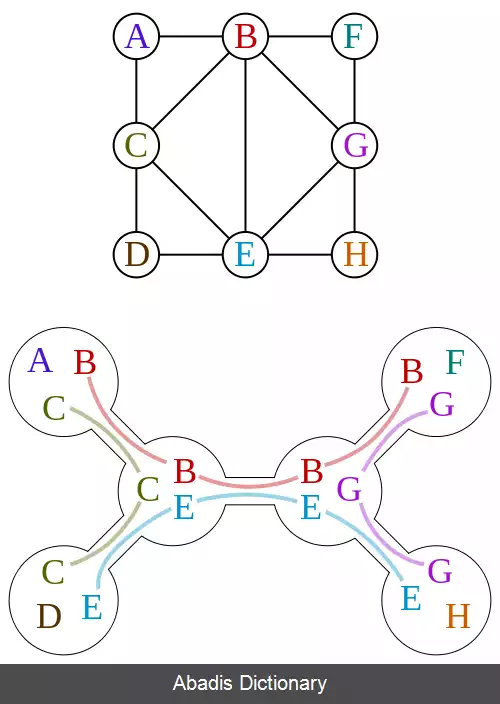
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتجزیهٔ درختی گراف G = ( V , E ) ، درختی است مانند T با رئوس X 1 , X 2 , . . . , X n ( به این رئوس کیف یا bag می گویند ) که در آن هر X i یک زیرمجموعه ای از V است که شرایط زیر را ارضا کند:
• اجتماع تمامی X i {\displaystyle X_{i}} ها، مجموعهٔ V {\displaystyle V} باشد.
• تمامی رئوس ( کیف های ) درخت که شامل راس v ∈ V {\displaystyle v\in V} هستند، تشکیل یک زیردرخت هم بند بدهند.
• برای هر یال مانند ( u , v ) {\displaystyle ( u, v ) } در گراف G {\displaystyle G} ، حداقل یک راس ( کیف ) مانند X i {\displaystyle X_{i}} در درخت باشد که شامل هر دو راس u {\displaystyle u} و v {\displaystyle v} است.
تجزیهٔ درختی یک گراف، یکتا نیست. بدیهی ترین تجزیهٔ درختی، قراردادن تمامی رئوس گراف در یک کیف است که در این صورت هر گراف یک تجزیه با عرض n − 1 دارد؛ بنابراین برای هر گراف تجزیه های درختی متعددی وجود دارد. عرض درختی یک تجزیهٔ درختی، برابر است با سایز بزرگ ترین کیف آن منهای یک. عرض درختی یک گراف نیز که با t w ( G ) نمایش داده می شود، برابرست با کم ترین عرض درختی میان تمامی تجریه های درختی آن گراف.
مثال: در شکل زیر گراف G و یک تجزیهٔ درختی از آن را می بینید. عرض این تجزیهٔ درختی، ۲ می باشد.
مثال: عرض درختی تمام درخت ها برابر با یک است.
تجزیهٔ درختی ( X i | i ∈ I , T ( I , F ) ) با عرض k نرم می گوییم اگر:
• ∀ i | X i | = k + 1 {\displaystyle \forall i\quad |X_{i}|=k+1}
• ∀ i , j ∈ F | X i ⋂ X j | = k {\displaystyle \forall {i, j}\in F\quad |X_{i}\bigcap X_{j}|=k}
نکته: هر تجزیهٔ درختی را می توان به یک تجزیهٔ درختی نرم تبدیل کرد.
فرض کنید ( X i | i ∈ I , T ( I , F ) ) یک تجزیهٔ درختی برای گراف G = ( V , E ) باشد به طوری که عرض آن حداکثر k باشد. می خواهیم الگوریتمی از O ( k 2 4 k | V | ) ارائه دهیم تا بزرگ ترین مجموعهٔ مستقل این گراف را پیدا کنیم.

wiki: عرض درخت
