در فیزیک اتمی، عدد کوانتومی اسپین یک عدد کوانتومی است که تکانه زاویه ای ذاتی ( یا تکانه زاویه ای اسپین یا تنها اسپین ) یک ذرهاست. عدد کوانتومی اسپین چهارمین عضو مجموعه ای از اعداد کوانتومی است ( عدد کوانتومی اصلی، عدد کوانتومی سمتی، عدد کوانتومی مغناطیسی و عدد کوانتومی اسپین ) که حالت کوانتومی یکتای یک الکترون را توصیف می کنند و توسط حرف s نمایش داده می شود. عدد کوانتومی اسپین تعیین کننده جهت گیری الکترون نسبت به میدان مغناطیسی خارجی است.
با حل یک معادله دیفرانسیل جزیی خاص، تکانه زاویه ای کوانتیزه شده به صورت زیر به دست می آید:
که
تصویر اسپین روی جهت دلخواه z به این صورت به دست می آید
که ms عدد کوانتومی اسپین ثانویه است که مقدار آن در محدوده s− تا s+ در گام های واحد تغییر می کند. یعنی 2 s + ۱ مقدار مختلف برای ms وجود دارد.
مقادیر مجاز برای s، تنها اعداد صحیح یا نیمه صحیح نامنفی هستند. فرمیون ها ( مانند الکترون، پروتونیا نوترون ) مقادیر اسپین نیمه صحیح دارند، در حالیکه بوزون ها ( مثلاً فوتونیا مزون ها ) مقادیر اسپین صحیح دارند. اثبات کامل msمساوی با مثبت منفی یک بروی دو
نظریه جبری اسپین در واقع رونوشتی از تکانه زاویه ای در مکانیک کوانتومی است. اول از همه، اسپین در رابطه جابه جایی بنیادی صدق می کند:
که εlmn نماد لوی - چیویتا ( نامتقارن ) است. یعنی به خاطر محدودیت حاصل از اصل عدم قطعیت، غیرممکن است که بتوانیم دو مختصات مختلف از اسپین را در یک زمان بدانیم
دوم اینکه، بردار ویژه های S 2 و S z در این رابطه ها صدق می کنند:
که S ± = S x ± i S y عملگرهای پیدایش و نابودی ( یا عملگرهای "بلندکردن" و "پایین آوردن" یا "بالاً و "پایین" ) هستند.
اثبات کامل ms مساوی با مثبت منفی یک بروی دو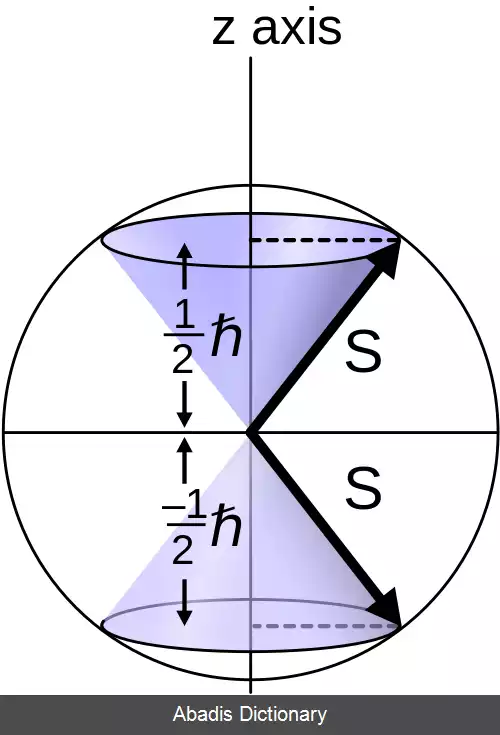
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبا حل یک معادله دیفرانسیل جزیی خاص، تکانه زاویه ای کوانتیزه شده به صورت زیر به دست می آید:
که
تصویر اسپین روی جهت دلخواه z به این صورت به دست می آید
که ms عدد کوانتومی اسپین ثانویه است که مقدار آن در محدوده s− تا s+ در گام های واحد تغییر می کند. یعنی 2 s + ۱ مقدار مختلف برای ms وجود دارد.
مقادیر مجاز برای s، تنها اعداد صحیح یا نیمه صحیح نامنفی هستند. فرمیون ها ( مانند الکترون، پروتونیا نوترون ) مقادیر اسپین نیمه صحیح دارند، در حالیکه بوزون ها ( مثلاً فوتونیا مزون ها ) مقادیر اسپین صحیح دارند. اثبات کامل msمساوی با مثبت منفی یک بروی دو
نظریه جبری اسپین در واقع رونوشتی از تکانه زاویه ای در مکانیک کوانتومی است. اول از همه، اسپین در رابطه جابه جایی بنیادی صدق می کند:
که εlmn نماد لوی - چیویتا ( نامتقارن ) است. یعنی به خاطر محدودیت حاصل از اصل عدم قطعیت، غیرممکن است که بتوانیم دو مختصات مختلف از اسپین را در یک زمان بدانیم
دوم اینکه، بردار ویژه های S 2 و S z در این رابطه ها صدق می کنند:
که S ± = S x ± i S y عملگرهای پیدایش و نابودی ( یا عملگرهای "بلندکردن" و "پایین آوردن" یا "بالاً و "پایین" ) هستند.
اثبات کامل ms مساوی با مثبت منفی یک بروی دو

wiki: عدد کوانتومی اسپین
