عدد مختلط
فرهنگستان زبان و ادب
دانشنامه عمومی
عدد مختلط[ ۱] ( به انگلیسی: Complex number ) یا عدد هم تافت عددی به شکل a + i b است که و اعداد حقیقی اند و i ، یکهٔ موهومی با خصوصیت i 2 = - 1 که ریشه x^2+1=0 است. عدد قسمت حقیقی و عدد قسمت موهومی نامیده و نوشته می شود:
• I m z = b {\displaystyle I_{m}z=b}
• R e z = a {\displaystyle R_{e}z=a}
اعداد حقیقی را می توان به عنوان اعداد مختلط با قسمت موهومی صفر در نظر گرفت، یعنی عدد حقیقی معادل است با عدد مختلط a + 0 i .
مجموعهٔ اعداد مختلط را به صورت C = { a + i b | a , b ∈ R , i 2 = − 1 } تعریف می کنیم.
دو عدد مختلط برابرند اگر و تنها اگر بخش های حقیقی و موهومی آن ها دو به دو با یکدیگر برابر باشند؛ یعنی a + b i = c + d i اگر و تنها اگر a = c و b = d. به عبارت دیگر دو عدد مختلط فقط زمانی برابرند که نمایش هندسی آن ها یک نقطه باشد.
مجموعه اعداد مختلط معمولاً با C نشان داده می شود. اعداد مختلط نیز می توانند جمع، تفریق، و ضرب شوند با در نظر گرفتن معادلهٔ i 2 = − 1
( a + b i ) + ( c + d i ) = ( a + c ) + ( b + d ) i
( a + b i ) − ( c + d i ) = ( a − c ) + ( b − d ) i
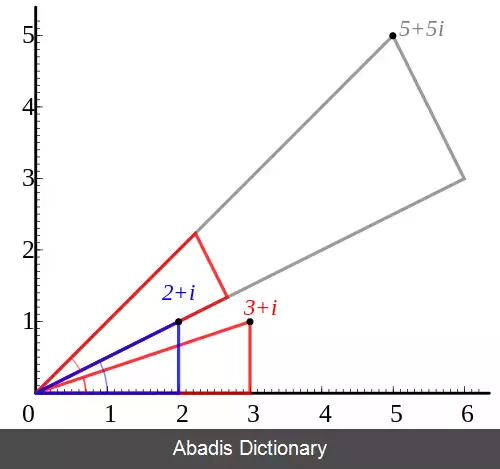
( a + b i ) ( c + d i ) = a c + b c i + a d i + b d i 2 = ( a c − b d ) + ( b c + a d ) i
تقسیم اعداد مختلط را نیز می توان تعریف کرد ( پایین را ببینید ) . بنابراین مجموعه اعداد مختلط یک میدان تشکیل می دهد که، در مقایسه با اعداد حقیقی، به طور جبری بسته است.
اعداد مختلط را می توان به صورت زوج های مرتب ( a, b ) از اعداد حقیقی نیز تعریف کرد. با اعمال:
( a , b ) + ( c , d ) = ( a + c , b + d )
( a , b ) ⋅ ( c , d ) = ( a c − b d , b c + a d ) .
بنابراین اعداد مختلط تشکیل یک میدان می دهند، میدان مختلط، که با C نشان داده می شود. از آنجایی که عدد مختلط a + bi به طور منحصربه فرد با یک زوج مرتب ( a, b ) نمایش داده می شود، پس اعداد مختلط یک تناظر یک به یک با نقاط در صفحه دارند. به آن صفحه مختلط گفته می شود. عدد حقیقی a را با عدد مختلط ( a, 0 ) نشان می دهیم و در این حالت میدان اعداد حقیقی R یک زیر میدان از C می شود. واحد موهومی i عدد مختلط ( 0, 1 ) است.
منظور از تقسیم دو عدد مختلط یعنی a + i b c + i d یافتن عددی است مثل x + i y که در تساوی a + i b = ( c + i d ) . ( x + i y ) صدق نماید، پس از محاسبه رابطه بالا داریم: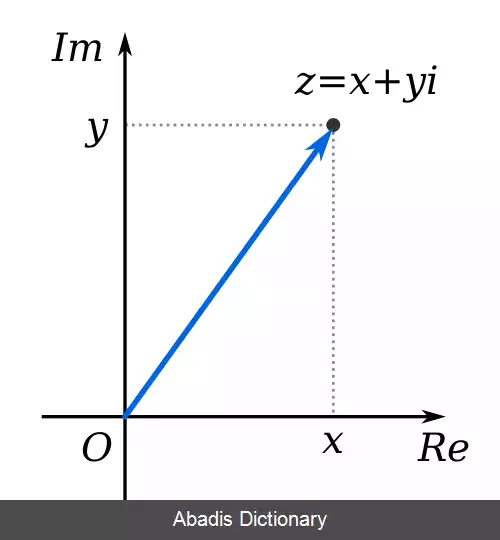
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف• I m z = b {\displaystyle I_{m}z=b}
• R e z = a {\displaystyle R_{e}z=a}
اعداد حقیقی را می توان به عنوان اعداد مختلط با قسمت موهومی صفر در نظر گرفت، یعنی عدد حقیقی معادل است با عدد مختلط a + 0 i .
مجموعهٔ اعداد مختلط را به صورت C = { a + i b | a , b ∈ R , i 2 = − 1 } تعریف می کنیم.
دو عدد مختلط برابرند اگر و تنها اگر بخش های حقیقی و موهومی آن ها دو به دو با یکدیگر برابر باشند؛ یعنی a + b i = c + d i اگر و تنها اگر a = c و b = d. به عبارت دیگر دو عدد مختلط فقط زمانی برابرند که نمایش هندسی آن ها یک نقطه باشد.
مجموعه اعداد مختلط معمولاً با C نشان داده می شود. اعداد مختلط نیز می توانند جمع، تفریق، و ضرب شوند با در نظر گرفتن معادلهٔ i 2 = − 1
( a + b i ) + ( c + d i ) = ( a + c ) + ( b + d ) i
( a + b i ) − ( c + d i ) = ( a − c ) + ( b − d ) i
( a + b i ) ( c + d i ) = a c + b c i + a d i + b d i 2 = ( a c − b d ) + ( b c + a d ) i
تقسیم اعداد مختلط را نیز می توان تعریف کرد ( پایین را ببینید ) . بنابراین مجموعه اعداد مختلط یک میدان تشکیل می دهد که، در مقایسه با اعداد حقیقی، به طور جبری بسته است.
اعداد مختلط را می توان به صورت زوج های مرتب ( a, b ) از اعداد حقیقی نیز تعریف کرد. با اعمال:
( a , b ) + ( c , d ) = ( a + c , b + d )
( a , b ) ⋅ ( c , d ) = ( a c − b d , b c + a d ) .
بنابراین اعداد مختلط تشکیل یک میدان می دهند، میدان مختلط، که با C نشان داده می شود. از آنجایی که عدد مختلط a + bi به طور منحصربه فرد با یک زوج مرتب ( a, b ) نمایش داده می شود، پس اعداد مختلط یک تناظر یک به یک با نقاط در صفحه دارند. به آن صفحه مختلط گفته می شود. عدد حقیقی a را با عدد مختلط ( a, 0 ) نشان می دهیم و در این حالت میدان اعداد حقیقی R یک زیر میدان از C می شود. واحد موهومی i عدد مختلط ( 0, 1 ) است.
منظور از تقسیم دو عدد مختلط یعنی a + i b c + i d یافتن عددی است مثل x + i y که در تساوی a + i b = ( c + i d ) . ( x + i y ) صدق نماید، پس از محاسبه رابطه بالا داریم:



wiki: عدد مختلط
دانشنامه آزاد فارسی
عدد مُختلط (complex number)
عدد مُختلط
در ریاضیات، عددی به شکلa + bi که در آن، a وb اعداد حقیقیاند وi نمایشگر(فرمول ۱)یا ریشۀ دوم -۱ است a . (i۲ = ۱)را قسمت حقیقی و bi را قسمت موهومی عدد مختلط می نامند.فرمول ۱:
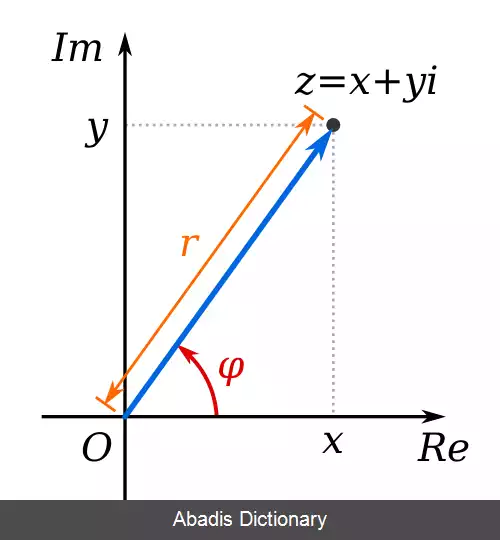
بعضی از معادله ها در جبر، ازجمله معادله ای به شکلx۲ + ۵ = ۰، بدون توسل به عددهای مختلط حل شدنی نیستند، زیرا اعداد حقیقی ریشه های دوم عددهای منفی را دربر نمی گیرند. برای جمع کردن دو یا چند عدد مختلط، قسمت های حقیقی آن ها را با هم و قسمت های موهومی آن ها را نیز باهم جمع می کنند.مثلاً (a + bi) + (c + di) = (a + c) + (b + d)i .عددهای مختلط را می توان به شکل تصویری در نمودار آرگان نمایش داد که در آن از مختصات دکارتی استفاده می کنند. در این نمودار، قسمت حقیقی این عددها روی محور x و قسمت موهومی آن ها روی محور yمشخص می شود. بنابراین، عددz = a + b به صورت نقطۀ (a,b) نمایش داده می شود. عددهای مختلط در زمینه های گوناگون علم، ازجمله نظریۀ جریان های متناوب در الکتریسیته، کاربرد دارند.
عدد مُختلط
در ریاضیات، عددی به شکلa + bi که در آن، a وb اعداد حقیقیاند وi نمایشگر(فرمول ۱)یا ریشۀ دوم -۱ است a . (i۲ = ۱)را قسمت حقیقی و bi را قسمت موهومی عدد مختلط می نامند.فرمول ۱:
بعضی از معادله ها در جبر، ازجمله معادله ای به شکلx۲ + ۵ = ۰، بدون توسل به عددهای مختلط حل شدنی نیستند، زیرا اعداد حقیقی ریشه های دوم عددهای منفی را دربر نمی گیرند. برای جمع کردن دو یا چند عدد مختلط، قسمت های حقیقی آن ها را با هم و قسمت های موهومی آن ها را نیز باهم جمع می کنند.مثلاً (a + bi) + (c + di) = (a + c) + (b + d)i .عددهای مختلط را می توان به شکل تصویری در نمودار آرگان نمایش داد که در آن از مختصات دکارتی استفاده می کنند. در این نمودار، قسمت حقیقی این عددها روی محور x و قسمت موهومی آن ها روی محور yمشخص می شود. بنابراین، عددz = a + b به صورت نقطۀ (a,b) نمایش داده می شود. عددهای مختلط در زمینه های گوناگون علم، ازجمله نظریۀ جریان های متناوب در الکتریسیته، کاربرد دارند.
wikijoo: عدد_مختلط
پیشنهاد کاربران
پیشنهادی ثبت نشده است. شما اولین نفر باشید
