در نظریه گراف، یک عامل از یک گراف G یک زیرگراف فراگیر است، برای مثال یک زیرگرافی که مجموعه رئوس برابری با G دارد. یک k - عامل از یک گراف یک زیرگراف فراگیر k - منتظم است و یک k - عامل بندی یال های گراف را به k - عامل های مستقل افراز می کند. گراف G را k - عامل پذیر می گویند هرگاه قابل k - عامل بندی شدن باشد. به طور کلی، یک ۱ - عامل یک تطابق کامل است، و یک ۱ - عامل بندی یک گراف k - منتظم یک رنگ آمیزی یالی با k رنگ است. یک ۲ - عامل مجموعه ای از دور ها است که تمام رئوس گراف را پوشش می دهند.
اگر یک گراف ۱ - عامل پذیر باشد، بنابراین باید یک گراف منتظم باشد. اما تمام گراف های منظم ۱ - عامل پذیر نیستند. یک گراف k - منتظم ۱ - عامل پذیر است اگر عدد رنگی k داشته باشد. به عنوان مثال:
• هر گراف دو بخشی منتظم. با استفاده از قضیه هال می توان نشان داد که یک گراف دو بخشی k - منتظم شامل یک تطابق کامل است. می توان با حذف تطابق کامل یک گراف دو بخشی ( k - ۱ ) - منتظم به دست آورد، و همین کار را تکرار کرد.
• هر گراف کامل با زوج راس ( زیر را ببینید )
اما گراف های k - منتظمی وجود دارد که عدد رنگی آن ها k+۱ است و این گراف ها ۱ - عامل پذیر نیستند. به عنوان مثال:
• هر گراف با فرد راس
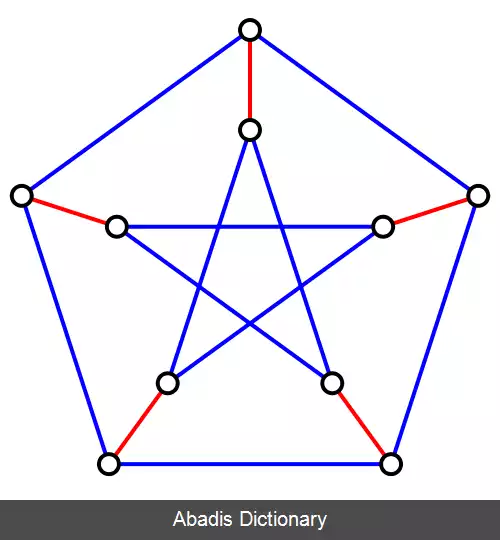
• گراف پترسن
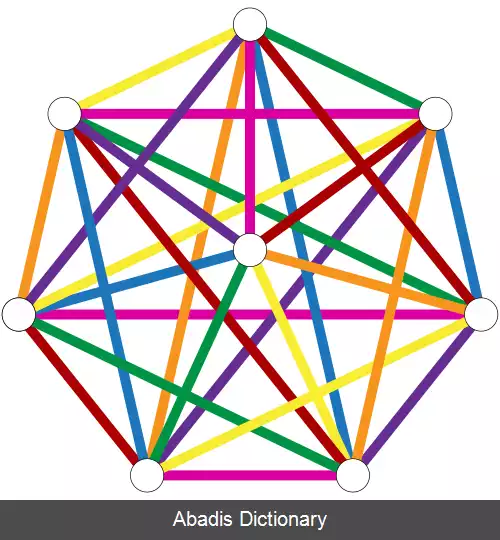
یک ۱ - عامل بندی از یک گراف کامل متناظر است با جفت ها در رقابت های دوره ای. ۱ - عاملبندی یک گراف کامل یک حالت خاص از قضیه بارانیای که به ۱ - عامل بندی یک ابرگراف کامل مربوط است. یکی از روش های ساختن یک ۱ - عامل بندی از یک گراف کامل این است که تمام رئوس به جز یکی را دور یک دایره بچینیم که یک چند ضلعی منتظم تشکیل بدهد، و راس باقیمانده را در وسط دایره قرار دهیم. اگر با این چیدمان رئوس، یک راه برای ساختن ۱ - عامل گراف انتخاب یک یال e از مرکز به یکی از رئوس چند ضلعی و انتخاب تمام یال های عمود بر آن. ۱ - عامل هایی که با این روش ساخته می شوند ۱ - عامل بندی گراف را تشکیل می دهند.
فرض کنید G یک گراف , k - منتظم با 2n راس باشد. اگر k به مقدار کافی بزرگ باشد، فهمیده می شود که G باید 1 - عامل پذیر باشد:
• اگر k = 2n – 1، آنگاه G یک گراف کامل K2n است و در نتیجه 1 - عامل پذیر.
• اگر k = 2n – 2، آنگاه G را می توان با حذف کردن یک تطابق کامل از K2n به دست آورد. G باز هم 1 - عامل پذیر است.
• ( Chetwyn & Hilton ( 1985 نشان دادند که اگر k ≥ 12n/7 باشد آنگاه G گرافی 1 - عامل پذیر است.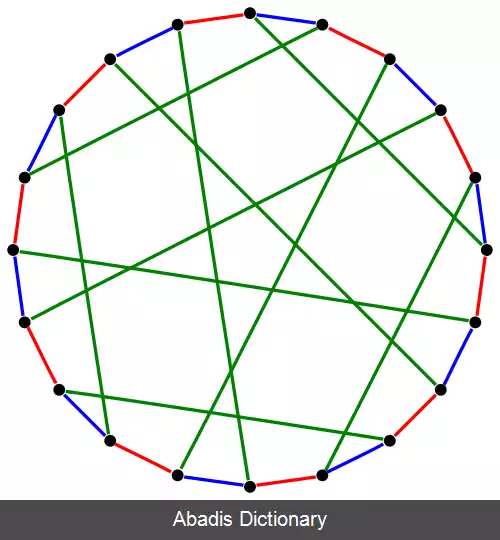
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاگر یک گراف ۱ - عامل پذیر باشد، بنابراین باید یک گراف منتظم باشد. اما تمام گراف های منظم ۱ - عامل پذیر نیستند. یک گراف k - منتظم ۱ - عامل پذیر است اگر عدد رنگی k داشته باشد. به عنوان مثال:
• هر گراف دو بخشی منتظم. با استفاده از قضیه هال می توان نشان داد که یک گراف دو بخشی k - منتظم شامل یک تطابق کامل است. می توان با حذف تطابق کامل یک گراف دو بخشی ( k - ۱ ) - منتظم به دست آورد، و همین کار را تکرار کرد.
• هر گراف کامل با زوج راس ( زیر را ببینید )
اما گراف های k - منتظمی وجود دارد که عدد رنگی آن ها k+۱ است و این گراف ها ۱ - عامل پذیر نیستند. به عنوان مثال:
• هر گراف با فرد راس
• گراف پترسن
یک ۱ - عامل بندی از یک گراف کامل متناظر است با جفت ها در رقابت های دوره ای. ۱ - عاملبندی یک گراف کامل یک حالت خاص از قضیه بارانیای که به ۱ - عامل بندی یک ابرگراف کامل مربوط است. یکی از روش های ساختن یک ۱ - عامل بندی از یک گراف کامل این است که تمام رئوس به جز یکی را دور یک دایره بچینیم که یک چند ضلعی منتظم تشکیل بدهد، و راس باقیمانده را در وسط دایره قرار دهیم. اگر با این چیدمان رئوس، یک راه برای ساختن ۱ - عامل گراف انتخاب یک یال e از مرکز به یکی از رئوس چند ضلعی و انتخاب تمام یال های عمود بر آن. ۱ - عامل هایی که با این روش ساخته می شوند ۱ - عامل بندی گراف را تشکیل می دهند.
فرض کنید G یک گراف , k - منتظم با 2n راس باشد. اگر k به مقدار کافی بزرگ باشد، فهمیده می شود که G باید 1 - عامل پذیر باشد:
• اگر k = 2n – 1، آنگاه G یک گراف کامل K2n است و در نتیجه 1 - عامل پذیر.
• اگر k = 2n – 2، آنگاه G را می توان با حذف کردن یک تطابق کامل از K2n به دست آورد. G باز هم 1 - عامل پذیر است.
• ( Chetwyn & Hilton ( 1985 نشان دادند که اگر k ≥ 12n/7 باشد آنگاه G گرافی 1 - عامل پذیر است.



wiki: عامل بندی گراف
