ضریب همبستگی رتبه ای اسپیرمن

ضریب همبستگی رتبه ای اسپیرمن [ ۱] آماره ای ناپارامتری برای سنجش ضریب همبستگی بین دو متغیر تصادفی است. این ضریب را معمولاً با ρ یا r s نشان می دهند.
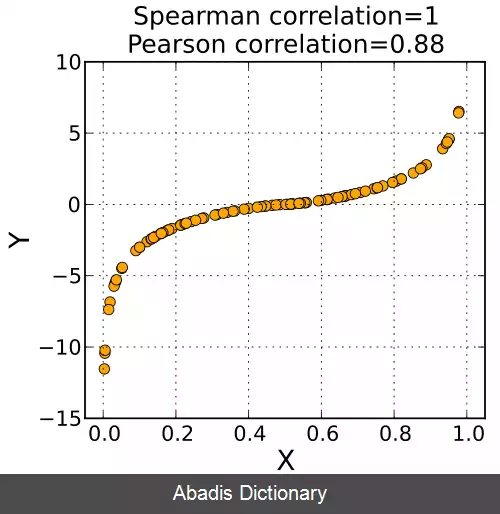
مقدار ضریب همبستگی رتبه ای اسپیرمن مبین قابلیت بیان یک متغیر به صورت تابعی یکنوا از متغیر دیگر است. همبستگی کامل پیرسون ( ۱+ یا ۱ - ) در جاییست که متغیری تابعی یکنوا از متغیر دیگر باشد. صفر بودن این ضریب دلیل استقلال متقابل است. لازم به ذکر است که از ضریب اسپیرمن تنها در شرایطی استفاده می شود که دادههای ورودی رتبه ای باشند. روش های دیگری مانند تای کندال را می توان به جای ضریب همبستگی اسپیرمن استفاده نمود که همانند روش اسپیرمن یک روش ناپارامتری محسوب می شود.
اگر n زوج داده به صورت ( X i , Y i ) داده شده باشند و رتبهٔ هر داده را به صورت ( x i , y i ) تعریف کنیم، ضریب اسپیرمن از طریق فرمول زیر محاسبه می گردد[ ۲] [ ۳] :
r s = 1 − 6 ∑ d i 2 n ( n 2 − 1 )
بطوریکه مقدار d i بیانگر فاصله بین دو رنک در مشاهدات است که از طریق فرمول d i = R ⁡ ( x i ) − R ⁡ ( y i ) محاسبه می گردد و n بیانگر تعداد مشاهدات است.
همچنین، این ضریب را می توان به صورت ضریب همبستگی پیرسون بین داده های رتبه بندی شده تعریف کرد. به عنوان مثال، اگر n زوج داده به صورت ( X i , Y i ) داده شده باشند، ابتدا رتبهٔ هر داده را به صورت ( x i , y i ) حساب کرده و سپس ضریب همبستگی اسپیرمن را به صورت زیر حساب می کنیم:
به داده های تکراری مقدار میانگین رتبه ها را اختصاص می دهیم. جدول زیر مثالی از محاسبهٔ رتبه را نشان می دهد:
فرض کنید دو سری دیتا رتبه ای به صورت جدول زیر وجود دارد. می خواهیم مقدار ضریب اسپیرمن را برای این دیتاها محاسبه نماییم.
مقدار ضریب اسپیرمن برای این دو سری دیتا 0. 5 خواهد بود که بیانگر مشابهت آنها می باشد. نحوه محاسبه ضریب اسپیرمن به صورت زیر است:
r s = 1 − 6 ∑ d i 2 n ( n 2 − 1 ) = 1 − 6 ∗ ( ( 1 − 1 ) 2 + ( 3 − 2 ) 2 + ( 2 − 3 ) 2 ) 3 ( 3 2 − 1 ) = 0. 5
در متلب، تابع corr برای این منظور است؛ مثلاً در کد زیر:
N=5;   % No. of nodes
x = randn ( N, 1 ) ; y = randn ( N, 1 ) ;
= corr ( x, y, 'type', 'Spearman' ) ;
z ( N, 2 ) =0; z ( :, 1 ) =x ( :, 1 ) ; z ( :, 2 ) =y ( :, 1 ) ; z2=sortrows ( z, 1 ) ; zx=z2 ( :, 1 ) ; zy=z2 ( :, 2 ) ;