ضرب هادامار (ماتریس ها). ضرب هادامار ( انگلیسی: Hadamard product ) یا ضرب درایه ای ریاضیات، عمل دوتایی است که دو ماتریس با ابعاد یکسان را گرفته و ماتریس دیگری تولید می کند که هر درایهٔ i j آن حاصلضرب درایه های i j آن دو ماتریس است. این ضرب را نباید با حاصلضرب رایجتر ماتریسها اشتباه گرفت. این ضرب به افتخار ریاضیدان فرانسوی ژاک آدامار، یا ریاضیدان آلمانی ایسای شور نامگذاری شده است. [ ۱]
برای دو ماتریس A و B که دارای ابعاد m × n هستند، [ ۲] ضرب هادامار آنها که با A ∘ B و یا A ⊙ B [ ۳] [ ۴] [ ۵] [ ۶] نمایش داده می شود ماتریسی با همان ابعاد ( یعنی m × n ) است که مقادیر آن به نحو پایین محاسبه می شوند:
برای ماتریسهایی که ابعاد متفاوت دارند این ضرب تعریف نشده است.
برای دو ماتریس A و B پایین که ابعاد 3 × 3 دارند ضرب هادامار آنها برابر است با:
∘ = .
• اگر A {\displaystyle A} و B {\displaystyle B} ماتریسهایی با ابعاد یکسان باشند رتبه ضرب هادامار از ضرب رتبه های دو ماتریس بیشتر نیست:
rank ( A ∘ B ) ≤ rank ( A ) rank ( B )
• اگر A {\displaystyle A} و B {\displaystyle B} و C {\displaystyle C} ماتریسهایی با ابعاد یکسان باشند و k {\displaystyle k} یک عدد حقیقی باشید آنگاه:
A ∘ B = B ∘ A , A ∘ ( B ∘ C ) = ( A ∘ B ) ∘ C , A ∘ ( B + C ) = A ∘ B + A ∘ C , ( k A ) ∘ B = A ∘ ( k B ) = k ( A ∘ B ) , A ∘ 0 = 0 ∘ A = 0 .
• برای بردارهای x {\displaystyle x} و y {\displaystyle y} و ماتریسهای قطری آنها D x {\displaystyle D_{x}} و D y {\displaystyle D_{y}} روابط پایین برقرار است:[ ۷]
x ∗ ( A ∘ B ) y = t r ( D x ∗ A D y B T ) ,
∑ i ( A ∘ B ) i j = ( B T A ) j j = ( A B T ) i i .
( y x ∗ ) ∘ A = D y A D x ∗
• برای مقادیر ویژه ماتریسهای A {\displaystyle A} و B {\displaystyle B} رابطه پایین برقرار است، در اینجا λ i ( A ) {\displaystyle \lambda _{i} ( A ) } i {\displaystyle i} - امین مقدار ویژه ماتریس A {\displaystyle A} است:[ ۸]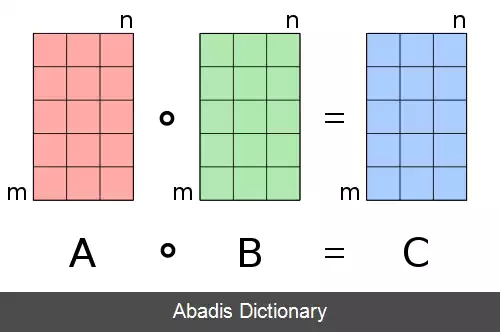
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبرای دو ماتریس A و B که دارای ابعاد m × n هستند، [ ۲] ضرب هادامار آنها که با A ∘ B و یا A ⊙ B [ ۳] [ ۴] [ ۵] [ ۶] نمایش داده می شود ماتریسی با همان ابعاد ( یعنی m × n ) است که مقادیر آن به نحو پایین محاسبه می شوند:
برای ماتریسهایی که ابعاد متفاوت دارند این ضرب تعریف نشده است.
برای دو ماتریس A و B پایین که ابعاد 3 × 3 دارند ضرب هادامار آنها برابر است با:
∘ = .
• اگر A {\displaystyle A} و B {\displaystyle B} ماتریسهایی با ابعاد یکسان باشند رتبه ضرب هادامار از ضرب رتبه های دو ماتریس بیشتر نیست:
rank ( A ∘ B ) ≤ rank ( A ) rank ( B )
• اگر A {\displaystyle A} و B {\displaystyle B} و C {\displaystyle C} ماتریسهایی با ابعاد یکسان باشند و k {\displaystyle k} یک عدد حقیقی باشید آنگاه:
A ∘ B = B ∘ A , A ∘ ( B ∘ C ) = ( A ∘ B ) ∘ C , A ∘ ( B + C ) = A ∘ B + A ∘ C , ( k A ) ∘ B = A ∘ ( k B ) = k ( A ∘ B ) , A ∘ 0 = 0 ∘ A = 0 .
• برای بردارهای x {\displaystyle x} و y {\displaystyle y} و ماتریسهای قطری آنها D x {\displaystyle D_{x}} و D y {\displaystyle D_{y}} روابط پایین برقرار است:[ ۷]
x ∗ ( A ∘ B ) y = t r ( D x ∗ A D y B T ) ,
∑ i ( A ∘ B ) i j = ( B T A ) j j = ( A B T ) i i .
( y x ∗ ) ∘ A = D y A D x ∗
• برای مقادیر ویژه ماتریسهای A {\displaystyle A} و B {\displaystyle B} رابطه پایین برقرار است، در اینجا λ i ( A ) {\displaystyle \lambda _{i} ( A ) } i {\displaystyle i} - امین مقدار ویژه ماتریس A {\displaystyle A} است:[ ۸]

wiki: ضرب هادامار (ماتریس ها)
