در علوم کامپیوتر تشخیص دور ( به انگلیسی: Cycle detection ) یا یافتن دور ( به انگلیسی: cycle finding ) مسئله ای الگوریتمی است که به بررسی پیدا کردن یک دور ( تکرار ) در توالی مقادیر یک تابع می کند.
برای هر تابع f که یک مجموعه متناهی S را به خودش، و هر مقدار اولیه x0 در S را، با توالی مقادیر تابع به صورت زیر نگاشت می کند
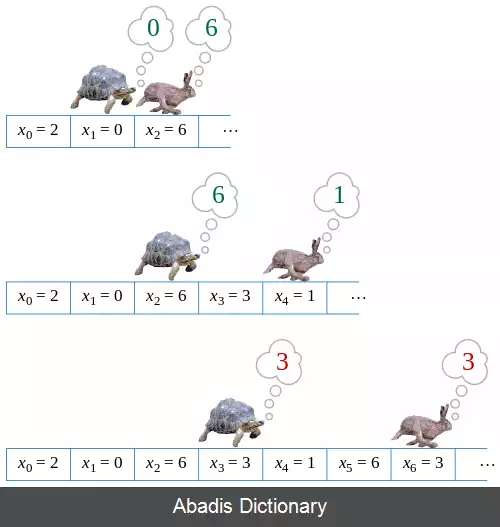
در نهایت مجبور به دو بار استفاده کردن از یک مقدار هستیم: باید جفت اندیس های مجزایی وجود داشته باشد به صورت i و j به طوری که xi = xj. هنگامی که این اتفاق می افتد، توالی باید همچنان به صورت دوره ای، با همان دنباله ای از مقادیر از xi تا xj − 1 تکرار شود. شناسایی دور مسئله پیدا کردن i و j با دانستن f و x0 می باشد.
چندین الگوریتم برای پیدا کردن دور به سرعت و با استفاده از حافظه اندک شناخته شده است. الگوریتم «لاک پشت و خرگوش» فلوید، الگوریتم حرکت دو اشاره گر در توالی مقادیر تابع با دو سرعت متفاوت می باشد تا در نهایت هر دو اشاره گر به یک مقدار برابر اشاره کنند. الگوریتم «برنت» بر اساس ایده جستجوی نمایی برقرار است. هر دو الگوریتم فلوید و برنت از تعداد ثابتی از سلول های حافظه استفاده می کنند، و هم چنین تعدادی از مقایسه و ارزیابی میان مقادیر تابع که متناسب با فاصله اولین تکرار از شروع توالی می باشد. دیگر الگوریتم ها استفاده بیشتر از حافظه در مقابل مقایسه های کمتر را پیشنهاد می دهند.
شناسایی دور شامل تست کیفیت مولد اعداد شبه تصادفی و تابع درهمساز رمزنگارانه، الگوریتم های نظریه اعداد رایانشی، تشخیص حلقه بی نهایت در برنامه های کامپیوتری و پیکربندی های متناوب در اتوماتای سلولی، و داده ساختارهای لیست پیوندی است.
این شکل یک تابع f که مقادیر مجموعه را می نگارد نشان می دهد
{S= {۰٬۱٬۲٬۳٬۴٬۵٬۶٬۷٬۸
را به خود. اگر یک نفر از x0 = ۲ شروع کند و مکرراً f را مورد اعمال قرار دهد دنباله ای از مقادیر زیر را مشاهده می کند
S را مجموعه متناهی دلخواهی فرض کنید، f تابعی دلخواه از S به خودش، و x0 هر عنصر دلخواه از Sباشد. برای هر i> 0، فرض می کنیم xi = f ( xi − 1 ) . فرض می کنیم μ کوچکترین اندیسی باشد به طوری که مقدار xμ به طور بینهایت در دنباله مقادیر xi ظاهر شود، و فرض می کنیم λ ( طول دور ) باشد کوچکترین عدد صحیح مثبت باشد به طوری که xμ = xλ + μ. تشخیص دور مسئله یافتن λ و μ می باشد. [ ۱]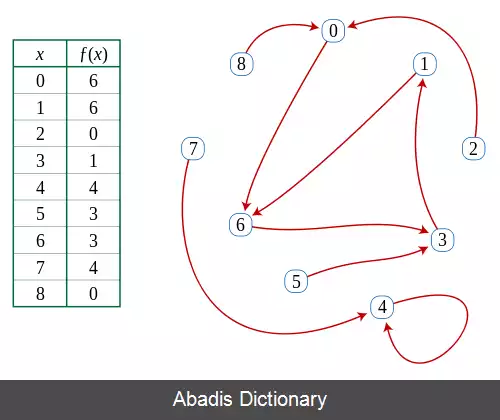
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبرای هر تابع f که یک مجموعه متناهی S را به خودش، و هر مقدار اولیه x0 در S را، با توالی مقادیر تابع به صورت زیر نگاشت می کند
در نهایت مجبور به دو بار استفاده کردن از یک مقدار هستیم: باید جفت اندیس های مجزایی وجود داشته باشد به صورت i و j به طوری که xi = xj. هنگامی که این اتفاق می افتد، توالی باید همچنان به صورت دوره ای، با همان دنباله ای از مقادیر از xi تا xj − 1 تکرار شود. شناسایی دور مسئله پیدا کردن i و j با دانستن f و x0 می باشد.
چندین الگوریتم برای پیدا کردن دور به سرعت و با استفاده از حافظه اندک شناخته شده است. الگوریتم «لاک پشت و خرگوش» فلوید، الگوریتم حرکت دو اشاره گر در توالی مقادیر تابع با دو سرعت متفاوت می باشد تا در نهایت هر دو اشاره گر به یک مقدار برابر اشاره کنند. الگوریتم «برنت» بر اساس ایده جستجوی نمایی برقرار است. هر دو الگوریتم فلوید و برنت از تعداد ثابتی از سلول های حافظه استفاده می کنند، و هم چنین تعدادی از مقایسه و ارزیابی میان مقادیر تابع که متناسب با فاصله اولین تکرار از شروع توالی می باشد. دیگر الگوریتم ها استفاده بیشتر از حافظه در مقابل مقایسه های کمتر را پیشنهاد می دهند.
شناسایی دور شامل تست کیفیت مولد اعداد شبه تصادفی و تابع درهمساز رمزنگارانه، الگوریتم های نظریه اعداد رایانشی، تشخیص حلقه بی نهایت در برنامه های کامپیوتری و پیکربندی های متناوب در اتوماتای سلولی، و داده ساختارهای لیست پیوندی است.
این شکل یک تابع f که مقادیر مجموعه را می نگارد نشان می دهد
{S= {۰٬۱٬۲٬۳٬۴٬۵٬۶٬۷٬۸
را به خود. اگر یک نفر از x0 = ۲ شروع کند و مکرراً f را مورد اعمال قرار دهد دنباله ای از مقادیر زیر را مشاهده می کند
S را مجموعه متناهی دلخواهی فرض کنید، f تابعی دلخواه از S به خودش، و x0 هر عنصر دلخواه از Sباشد. برای هر i> 0، فرض می کنیم xi = f ( xi − 1 ) . فرض می کنیم μ کوچکترین اندیسی باشد به طوری که مقدار xμ به طور بینهایت در دنباله مقادیر xi ظاهر شود، و فرض می کنیم λ ( طول دور ) باشد کوچکترین عدد صحیح مثبت باشد به طوری که xμ = xλ + μ. تشخیص دور مسئله یافتن λ و μ می باشد. [ ۱]


wiki: شناسایی دور
