در ترکیبیات ( به انگلیسی: Combinatorics ) ، دوگانه شمردن ( به انگلیسی: Double counting ) ، که به آن شمارش مضاعف نیز گفته می شود، یک روش اثبات ترکیبیاتی برای نشان دادن آن است که دو عبارت با یکدیگر برابرند؛ با ادعا کردن این که دو روش برای شمردن اندازهٔ یک مجموعه وجود دارد. در این روش، که ون لینت و ویلسون آن را «یکی از مهمترین ابزارها در ترکیبیات» خوانده اند. به این صورت عمل می کنیم که یک مجموعه متناهی X عضوی را از دو دیدگاه متفاوت توصیف می کنیم و به دو عبارت مجزا می رسیم. چون هر دو عبارت برابر اندازهٔ یک مجموعه هستند پس با یکدیگر برابرند.
یک نمونه از روش دوگانه شمردن، شمردن تعداد راه هایی است که می توان یک دسته از افراد را از n نفر تشکیل داد، با این اجازه که هر عضو این مجموعه ( حتی صفر تای آن ها ) می تواند عضو این دسته باشد. به این صورت، داریم تعداد زیرمجموعه های که یک مجموعهٔ n عضوی می تواند داشته باشد می شماریم. یک راه برای تشکیل یک دسته این است که از هر شخص بخواهیم تا انتخاب کند که باشد یا نباشد. هر شخص دو جواب دارد - بله یا خیر - و این پاسخ از انتخاب دیگر افراد مستقل است؛ بنابراین تعداد حالات با 2 × 2 × . . . × 2 = 2 n برابر است. راه دیگر این است که اندازهٔ مجموعه باید عددی بین ۰ تا n باشد. پس برای هر k ممکن، تعداد راه های ممکن برای تشکیل یک دسته k عضوی از n نفر برابر ضریب دو جمله ای است.
از این رو کل تعداد دسته های ممکن برابر مجموع ضرایب دوجله ای روی k = 0, 1, 2, . . . n است. برابر قرار دادن دو عبارت یک اتحاد را می دهد.
که یک حالت خاص از بسط دو جمله ای است. با یک روش دوگانه شماری مشابه می توان به یک اتحاد تعمیم یافته رسید
یک تئوری دیگر که معمولاً با دوگانه شماری اثبات می شود. بحث این گونه مطرح می شود که هر گراف ساده شامل ( به انگلیسی: undirected graph ) تعداد زوجی راس با درجه ( به انگلیسی: degree ) فرد دارد. یعنی، تعداد رئوسی که تعداد فردی یال دارند باید زوج باشد. در اصطلاحات محاوره ای تر، در یک مهمانی از افراد که تعدادی از آن ها با یکدیگر دست می دهند، تعداد زوجی از افراد باید با تعداد فردی از افراد دیگر دست دست داده باشند؛ به همین دلیل، به این نتیجه لم دست دادن نیز می گویند.
برای اثبات این با دوگانه شماری، راس ( d ( v را درجه راس v در نظر بگیرید. تعداد ظهور یال ها روی راس ها در یک گراف ممکن به دو روش شمرده شود:باجمع کردن درجات تمامی رئوس، یا با جمع کردن دو ظهور به ازای هر یال؛ بنابراین: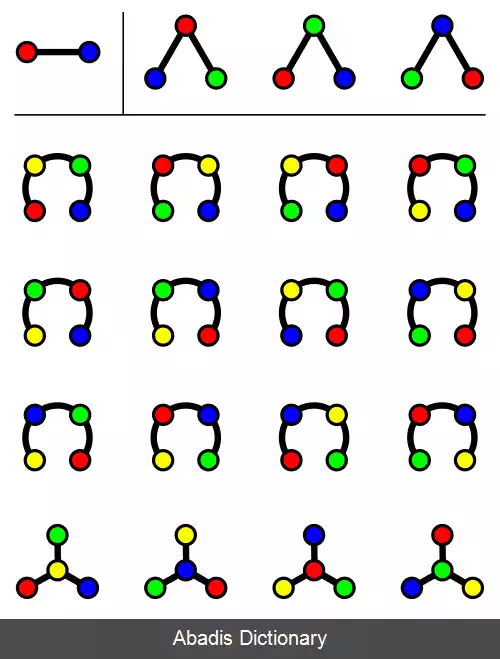
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک نمونه از روش دوگانه شمردن، شمردن تعداد راه هایی است که می توان یک دسته از افراد را از n نفر تشکیل داد، با این اجازه که هر عضو این مجموعه ( حتی صفر تای آن ها ) می تواند عضو این دسته باشد. به این صورت، داریم تعداد زیرمجموعه های که یک مجموعهٔ n عضوی می تواند داشته باشد می شماریم. یک راه برای تشکیل یک دسته این است که از هر شخص بخواهیم تا انتخاب کند که باشد یا نباشد. هر شخص دو جواب دارد - بله یا خیر - و این پاسخ از انتخاب دیگر افراد مستقل است؛ بنابراین تعداد حالات با 2 × 2 × . . . × 2 = 2 n برابر است. راه دیگر این است که اندازهٔ مجموعه باید عددی بین ۰ تا n باشد. پس برای هر k ممکن، تعداد راه های ممکن برای تشکیل یک دسته k عضوی از n نفر برابر ضریب دو جمله ای است.
از این رو کل تعداد دسته های ممکن برابر مجموع ضرایب دوجله ای روی k = 0, 1, 2, . . . n است. برابر قرار دادن دو عبارت یک اتحاد را می دهد.
که یک حالت خاص از بسط دو جمله ای است. با یک روش دوگانه شماری مشابه می توان به یک اتحاد تعمیم یافته رسید
یک تئوری دیگر که معمولاً با دوگانه شماری اثبات می شود. بحث این گونه مطرح می شود که هر گراف ساده شامل ( به انگلیسی: undirected graph ) تعداد زوجی راس با درجه ( به انگلیسی: degree ) فرد دارد. یعنی، تعداد رئوسی که تعداد فردی یال دارند باید زوج باشد. در اصطلاحات محاوره ای تر، در یک مهمانی از افراد که تعدادی از آن ها با یکدیگر دست می دهند، تعداد زوجی از افراد باید با تعداد فردی از افراد دیگر دست دست داده باشند؛ به همین دلیل، به این نتیجه لم دست دادن نیز می گویند.
برای اثبات این با دوگانه شماری، راس ( d ( v را درجه راس v در نظر بگیرید. تعداد ظهور یال ها روی راس ها در یک گراف ممکن به دو روش شمرده شود:باجمع کردن درجات تمامی رئوس، یا با جمع کردن دو ظهور به ازای هر یال؛ بنابراین:


wiki: شمارش مضاعف
