در هندسه تصویری، قضیهٔ ژیلبرت پاسکال بیان می کند که اگر روی یک مقطع مخروطی ( دایره، بیضی، سهمی یا هذلولی ) شش نقطه اختیار کنیم، و به ترتیب A تا F نامگذاری کنیم، نقاط تقاطع AB با DE و BC با EF و CD با FA ( جفت های متقابل ) بر روی یک خط راست قرار دارند و بالعکس. این قضیه در صفحهٔ اقلیدسی بر قرار است، منتها برای وقتی جفت متقابل موازی یکدیگرند نیاز به رفع اختلاف است.
پاسکال این قضیه را در سن ۱۶ سالگی اثبات کرد البته ابتدا برای دایره استفاده گردید. سپس نشان داده که به وسیلهٔ تصویر کردن مخروطی، قابل تعمیم و تحقیق است. او در کتابی به نام"مقاله دربارهٔ مقاطع مخروطی" نوشته است که توانسته بیش از ۴۰۰ حکم از خواص مقاطع مخروطی - شامل تمام آثار آپولونیوس - را به عنوان فرع و نتیجه از این قضیه استنباط کند. این کتاب منتشر نشده، اما لایب نیتس نسخهٔ خطی آن را دیده است.
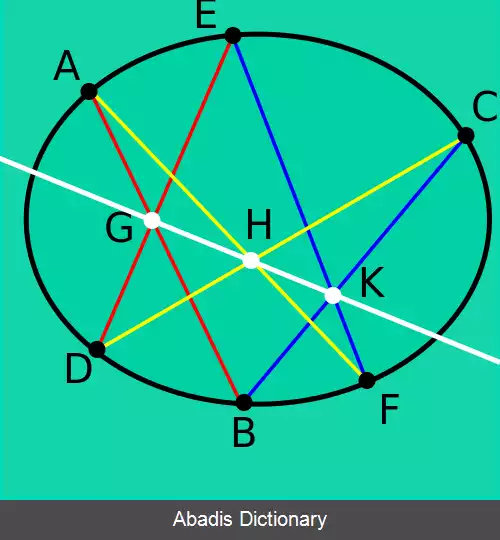
در شش ضلعی ABCDEF، اگر AC با BD در G، BE با CF در Hو AE با DF درI یکدیگر را قطع کنند:[ ۱] G B ¯ G D ¯ × I D ¯ I F ¯ × H F ¯ H C ¯ × G C ¯ G A ¯ × I A ¯ I F ¯ × H E ¯ H B ¯ = 1
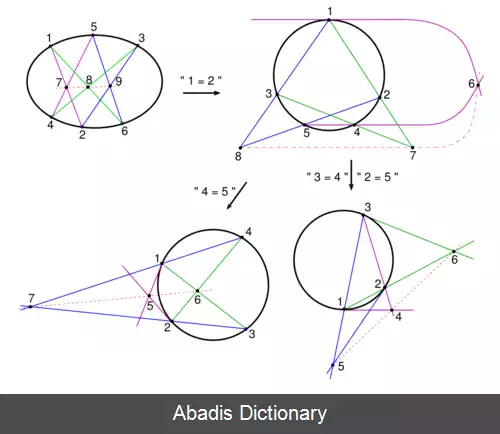
قضیهٔ پاسکال برای ۵، ۴ و ۳ نقطه هم صادق است.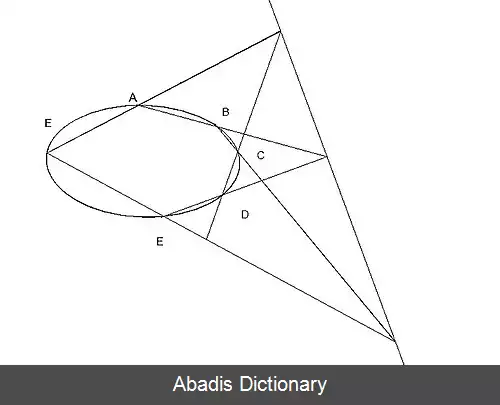
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفپاسکال این قضیه را در سن ۱۶ سالگی اثبات کرد البته ابتدا برای دایره استفاده گردید. سپس نشان داده که به وسیلهٔ تصویر کردن مخروطی، قابل تعمیم و تحقیق است. او در کتابی به نام"مقاله دربارهٔ مقاطع مخروطی" نوشته است که توانسته بیش از ۴۰۰ حکم از خواص مقاطع مخروطی - شامل تمام آثار آپولونیوس - را به عنوان فرع و نتیجه از این قضیه استنباط کند. این کتاب منتشر نشده، اما لایب نیتس نسخهٔ خطی آن را دیده است.
در شش ضلعی ABCDEF، اگر AC با BD در G، BE با CF در Hو AE با DF درI یکدیگر را قطع کنند:[ ۱] G B ¯ G D ¯ × I D ¯ I F ¯ × H F ¯ H C ¯ × G C ¯ G A ¯ × I A ¯ I F ¯ × H E ¯ H B ¯ = 1
قضیهٔ پاسکال برای ۵، ۴ و ۳ نقطه هم صادق است.



wiki: شش ضلعی عرفانی
