شبکه پسماند
با در اختیار داشتن شبکه شاره G و جریان f ، شبکه پسماند Gf ، متشکل از رئوس گراف و ظرفیت هر یک از آن ها می باشد. هر یال در شبکه ی جریان، ممکن است قادر به عبور مقدار جریان بیشتری از خود باشد. این مقدار، معادل تفاضل ظرفیت و جریان گذرنده از آن یال است. چنان چه این مقدار مثبت باشد، یال مورد نظر با مقدار ظرفیت پسماند خود در Gf قرار می گیرد. مقدار ظرفیت پسماند برای هر یال مانند ( u, v ) را با c f ( u , v ) نمایش داده که مقدار آن از رابطه ی c f ( u , v ) = c ( u , v ) − f ( u , v ) قابل محاسبه است. چنان چه ظرفیت یالی، برابر جریان گذرنده از آن باشد، c f ( u , v ) = 0 بوده و در گراف پسماند قرار نمی گیرد. همچنین شبکه ی پسماند ممکن است شامل یال هایی باشد که در گراف موجود نیستند. هم چنان که در بسیاری از الگوریتم ها، نیاز به افزایش مقدار جریان عبوری از یک یال وجود دارد، کاهش مقدار جریان عبوری نیز در برخی از آنها مانند الگوریتم فورد–فالکرسون مورد استفاده قرار می گیرد. جهت نمایش کاهش جریان عبوری مثبت f ( u , v ) در گراف G ، یال ( v , u ) را با ظرفیت پسماند c f ( v , u ) = f ( u , v ) در G f قرار می دهیم. به طور خلاصه، مقدار ظرفیت پسماند به شکل زیر محاسبه می شود:
• اگر ( u , v ) ∈ E {\displaystyle ( u, v ) \in E} آنگاه c f ( u , v ) = c ( u , v ) − f ( u , v ) {\displaystyle c_{f} ( u, v ) =c ( u, v ) - f ( u, v ) }
• اگر ( u , v ) ∉ E {\displaystyle ( u, v ) \not \in E} آنگاه c f ( u , v ) = f ( v , u ) {\displaystyle c_{f} ( u, v ) =f ( v, u ) }
• در غیر این صورت c f ( u , v ) = 0 {\displaystyle c_{f} ( u, v ) =0}
با استفاده از جریان در شبکه پسماند، می توان مقدار جریان قابل افزودن به جریان شار اصلی را محاسبه نمود. اگر شار شبکه G را با f و شار گذرنده از شبکه پسماند متعلق به آن یعنی G f را با f ′ نمایش دهیم، f ↑ f ′ یک جریان افزاینده برای f توسط f ′ خواهد بود. جریان افزاینده در حقیقت یک تابع از V × V به اعداد حقیقی است که مقدار آن به شکل زیر محاسبه می شود:
• اگر ( u , v ) ∈ E {\displaystyle ( u, v ) \in E} آنگاه: ( f ↑ f ′ ) ( u , v ) = f ( u , v ) + f ′ ( u , v ) − f ′ ( v , u ) {\displaystyle ( f\uparrow f' ) ( u, v ) =f ( u, v ) +f' ( u, v ) - f' ( v, u ) }
• در غیر این صورت ( f ↑ f ′ ) ( u , v ) = 0 {\displaystyle ( f\uparrow f' ) ( u, v ) =0}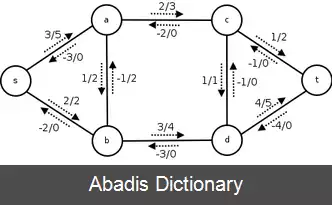
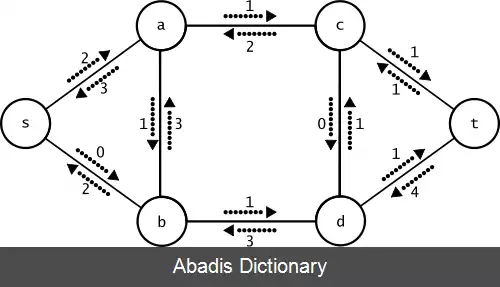
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبا در اختیار داشتن شبکه شاره G و جریان f ، شبکه پسماند Gf ، متشکل از رئوس گراف و ظرفیت هر یک از آن ها می باشد. هر یال در شبکه ی جریان، ممکن است قادر به عبور مقدار جریان بیشتری از خود باشد. این مقدار، معادل تفاضل ظرفیت و جریان گذرنده از آن یال است. چنان چه این مقدار مثبت باشد، یال مورد نظر با مقدار ظرفیت پسماند خود در Gf قرار می گیرد. مقدار ظرفیت پسماند برای هر یال مانند ( u, v ) را با c f ( u , v ) نمایش داده که مقدار آن از رابطه ی c f ( u , v ) = c ( u , v ) − f ( u , v ) قابل محاسبه است. چنان چه ظرفیت یالی، برابر جریان گذرنده از آن باشد، c f ( u , v ) = 0 بوده و در گراف پسماند قرار نمی گیرد. همچنین شبکه ی پسماند ممکن است شامل یال هایی باشد که در گراف موجود نیستند. هم چنان که در بسیاری از الگوریتم ها، نیاز به افزایش مقدار جریان عبوری از یک یال وجود دارد، کاهش مقدار جریان عبوری نیز در برخی از آنها مانند الگوریتم فورد–فالکرسون مورد استفاده قرار می گیرد. جهت نمایش کاهش جریان عبوری مثبت f ( u , v ) در گراف G ، یال ( v , u ) را با ظرفیت پسماند c f ( v , u ) = f ( u , v ) در G f قرار می دهیم. به طور خلاصه، مقدار ظرفیت پسماند به شکل زیر محاسبه می شود:
• اگر ( u , v ) ∈ E {\displaystyle ( u, v ) \in E} آنگاه c f ( u , v ) = c ( u , v ) − f ( u , v ) {\displaystyle c_{f} ( u, v ) =c ( u, v ) - f ( u, v ) }
• اگر ( u , v ) ∉ E {\displaystyle ( u, v ) \not \in E} آنگاه c f ( u , v ) = f ( v , u ) {\displaystyle c_{f} ( u, v ) =f ( v, u ) }
• در غیر این صورت c f ( u , v ) = 0 {\displaystyle c_{f} ( u, v ) =0}
با استفاده از جریان در شبکه پسماند، می توان مقدار جریان قابل افزودن به جریان شار اصلی را محاسبه نمود. اگر شار شبکه G را با f و شار گذرنده از شبکه پسماند متعلق به آن یعنی G f را با f ′ نمایش دهیم، f ↑ f ′ یک جریان افزاینده برای f توسط f ′ خواهد بود. جریان افزاینده در حقیقت یک تابع از V × V به اعداد حقیقی است که مقدار آن به شکل زیر محاسبه می شود:
• اگر ( u , v ) ∈ E {\displaystyle ( u, v ) \in E} آنگاه: ( f ↑ f ′ ) ( u , v ) = f ( u , v ) + f ′ ( u , v ) − f ′ ( v , u ) {\displaystyle ( f\uparrow f' ) ( u, v ) =f ( u, v ) +f' ( u, v ) - f' ( v, u ) }
• در غیر این صورت ( f ↑ f ′ ) ( u , v ) = 0 {\displaystyle ( f\uparrow f' ) ( u, v ) =0}


wiki: شبکه پسماند
