برای تحلیل شبکه های حمل و نقل که وسیله حمل کالاها از مراکز تولید به بازار هستند یا شبکه های مخابراتی که داده ها را منتقل می کنند یا شبکه های رایانه ای یا شبکه خطوط انتقال گاز در شهرها را توسط گراف های سودار مورد تحلیل قرار می دهیم. مشاهده می شود که در این گونه شبکه ها، گراف معادل نیازمند ساختار یا مؤلفه هایی اضافی است؛ مثلاً به طور خاص بایستی هر یال سودار دارای عدد مثبت یا صفری به عنوان میزان ظرفیت آن باشد که این عدد نشان دهنده ظرفیت حمل داده در این خط است. تحلیل شبکه های شاره دارای دامنه وسیعی از این کاربردهاست.
در ۱۹۳۰ بیان مسئله راه آهن شوروی موجب تحریک آمریکایی ها برای حل این مسئله شد. در ابتدای سال ۱۹۵۵این مسئله توسط تی. ای. هریس[ ۱] به صورت دیگری بیان شد: شبکهٔ راه آهنی را در نظر بگیرید که دو شهر را از طریق تعدادی شهرهای میانی به هم وصل کرده است. در این شبکه، هر مسیر دارای عددی است که نشان دهنده ظرفیت انتقال آن مسیر می باشد. وضعیت پایداری را در نظر بگیرید؛ بیشترین شاره ای که می تواند از هر شهر دلخواه خارج شود و به شهر مشخص دیگری وارد شود، چقدر است؟ فورد و فالکرسون بیان کردند که هریس در سال ۹۵ یک مدل ساده از جریان ترافیک در این مسئله ارائه کرد.
گراف سودار ( G= ( V, E را یک شبکه شاره می نامیم اگر:
• اولاً هر یال v, u ) € E ) دارای یک میزان ظرفیت غیر منفی یعنیc ( u, v ) ≥۰ است. برای زوج های ( u, v ) که در E وجود ندارند ظرفیت آن ها را صفر فرض می کنیم. همچنین چنانچه E دارای یالی مانند ( u, v ) باشد، یال ( v, u ) در جهت مخالف آن در گراف موجود نباشد.
• ثانیاً دو راس مجزای s با نام منبع و t با نام چاهک در این گراف وجود دارد که s فقط مبدأ چند یال و t فقط مقصد چند یال است و هر راس دیگر گراف در مسیری از s به t قرار می گیرد.
اگر ( G= ( V, E یک شبکه شاره با منبع s و چاهک t باشد، یک شارش در G f:V×V تابع است که سه شرط زیر را ارضا می کند:
• ۱»شرط محدودیت ظرفیت: برای هر u, v€ V بایستی ( f ( u, v ) ≤c ( u, v باشد.
• ۲»شرط تقارن شارش: برای هر u, v€ V بایستی ( f ( u, v ) = - f ( v, u باشد.
• ۳»شرط بقای شارش: برای هر {u€V – {s، t بایستی v∈V ) f ( u, v ) =۰ ) _∑ باشد.
مقدار شارش در هر یال می تواند عدد حقیقی منفی یا مثبت یا صفر باشد. اندازه شارش f را مساوی مقدار شارش خروجی از منبع تعریف می کنیم؛ یعنی: ( f| = ∑_ ( v∈V ) f ( s, v|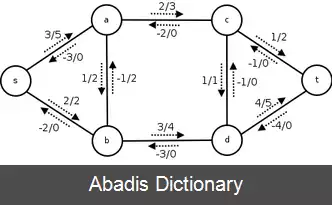
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر ۱۹۳۰ بیان مسئله راه آهن شوروی موجب تحریک آمریکایی ها برای حل این مسئله شد. در ابتدای سال ۱۹۵۵این مسئله توسط تی. ای. هریس[ ۱] به صورت دیگری بیان شد: شبکهٔ راه آهنی را در نظر بگیرید که دو شهر را از طریق تعدادی شهرهای میانی به هم وصل کرده است. در این شبکه، هر مسیر دارای عددی است که نشان دهنده ظرفیت انتقال آن مسیر می باشد. وضعیت پایداری را در نظر بگیرید؛ بیشترین شاره ای که می تواند از هر شهر دلخواه خارج شود و به شهر مشخص دیگری وارد شود، چقدر است؟ فورد و فالکرسون بیان کردند که هریس در سال ۹۵ یک مدل ساده از جریان ترافیک در این مسئله ارائه کرد.
گراف سودار ( G= ( V, E را یک شبکه شاره می نامیم اگر:
• اولاً هر یال v, u ) € E ) دارای یک میزان ظرفیت غیر منفی یعنیc ( u, v ) ≥۰ است. برای زوج های ( u, v ) که در E وجود ندارند ظرفیت آن ها را صفر فرض می کنیم. همچنین چنانچه E دارای یالی مانند ( u, v ) باشد، یال ( v, u ) در جهت مخالف آن در گراف موجود نباشد.
• ثانیاً دو راس مجزای s با نام منبع و t با نام چاهک در این گراف وجود دارد که s فقط مبدأ چند یال و t فقط مقصد چند یال است و هر راس دیگر گراف در مسیری از s به t قرار می گیرد.
اگر ( G= ( V, E یک شبکه شاره با منبع s و چاهک t باشد، یک شارش در G f:V×V تابع است که سه شرط زیر را ارضا می کند:
• ۱»شرط محدودیت ظرفیت: برای هر u, v€ V بایستی ( f ( u, v ) ≤c ( u, v باشد.
• ۲»شرط تقارن شارش: برای هر u, v€ V بایستی ( f ( u, v ) = - f ( v, u باشد.
• ۳»شرط بقای شارش: برای هر {u€V – {s، t بایستی v∈V ) f ( u, v ) =۰ ) _∑ باشد.
مقدار شارش در هر یال می تواند عدد حقیقی منفی یا مثبت یا صفر باشد. اندازه شارش f را مساوی مقدار شارش خروجی از منبع تعریف می کنیم؛ یعنی: ( f| = ∑_ ( v∈V ) f ( s, v|

wiki: شبکه شاره
