سیستم خودگردان (ریاضیات). در ریاضیات، یک سیستم خودگردان یا معادله دیفرانسیل خودگردان، سیستمی از معادلات دیفرانسیل معمولی است که صریحاً به متغیر مستقل بستگی ندارد. هنگامی که متغیر زمان است، به آنها سیستم های تغییرناپذیر با زمان نیز گفته می شود.
بسیاری از قوانین در فیزیک، که متغیر مستقل معمولاً به عنوان زمان فرض می شود، به عنوان سیستم های خودگردان بیان می شوند زیرا فرض بر این است که قوانین طبیعت که اکنون وجود دارد با هر نقطه از گذشته یا آینده یکسان است.
سیستم های خودگردان با سیستم های دینامیکی ارتباط تنگاتنگی دارند. هر سیستم خودگردانی را می توان به یک سیستم دینامیکی تبدیل کرد و با استفاده از فرضیات بسیار ضعیف، یک سیستم دینامیکی می تواند به یک سیستم خودگردان تبدیل شود[ نیازمند منبع]
سیستم خودگردان سیستمی از معادلات دیفرانسیل معمولی است به این شکل
که x مقادیر را در فضای اقلیدسی n بُعدی می گیرد؛ t اغلب به عنوان زمان تعبیر می شود.
از سیستم معادلات دیفرانسیل شکلی متمایز می شود
که در آن قانون حاکم بر تکامل سیستم فقط به وضعیت فعلی سیستم بستگی ندارد بلکه به پارامتر t نیز بستگی دارد، که اغلب به عنوان زمان تفسیر می شود؛ چنین سیستم هایی بنا به تعریف خودگردان نیستند.
اجازه دهید x 1 ( t ) یک جواب منحصر به فرد از مسئله مقدار اولیه برای یک سیستم خودگردان باشد
سپس x 2 ( t ) = x 1 ( t − t 0 ) حل می کند
در واقع، نمایان گر s = t − t 0 ما داریم x 1 ( s ) = x 2 ( t ) و d s = d t ، بدین ترتیب
برای این شرایط اولیه، این اثبات بدیهی است،
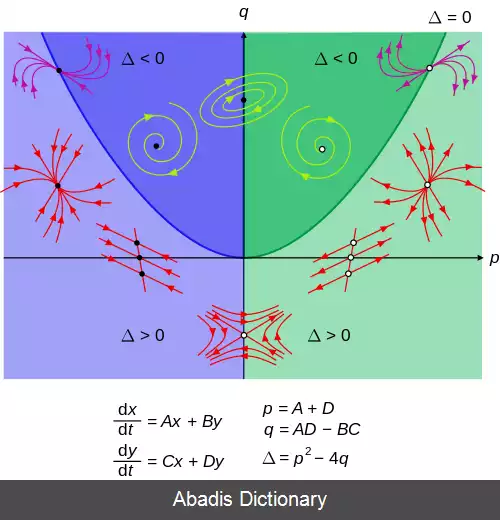
سیستم های خودگردان را می توان با استفاده از فضای فاز به صورت کیفی تحلیل کرد. در حالت یک متغیره، این خط فاز است.
روش های زیر برای معادلات دیفرانسیل خودگردان یک بعدی اعمال می شود. هر معادله یک - بُعدی از مرتبه n برابر است با یک دستگاه مرتبه اول n - بُعدی ( همان طور که در معادله دیفرانسیل معمولی # کاهش به سیستم مرتبه اول شرح داده شده است ) ، اما لزوماً برعکس برقرار نیست.
معادله خودگردان مرتبه اول
جداشدنی است، بنابراین با مرتب سازی مجدد در فرم انتگرالی به راحتی قابل حل است
معادله خودگردان مرتبه دوم
دشوارتر است، اما با معرفی متغیر جدید می توان آن را حل کرد
و بیان مشتق دوم از x ( از طریق قاعده زنجیره ای ) به عنوان
به طوری که معادله اصلی شود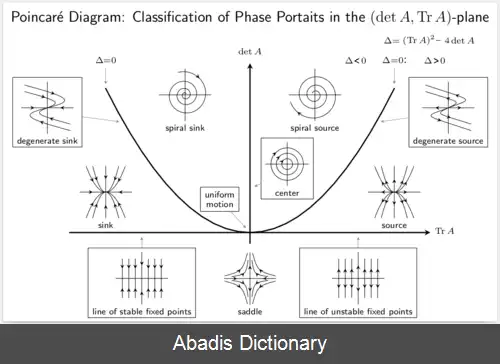
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبسیاری از قوانین در فیزیک، که متغیر مستقل معمولاً به عنوان زمان فرض می شود، به عنوان سیستم های خودگردان بیان می شوند زیرا فرض بر این است که قوانین طبیعت که اکنون وجود دارد با هر نقطه از گذشته یا آینده یکسان است.
سیستم های خودگردان با سیستم های دینامیکی ارتباط تنگاتنگی دارند. هر سیستم خودگردانی را می توان به یک سیستم دینامیکی تبدیل کرد و با استفاده از فرضیات بسیار ضعیف، یک سیستم دینامیکی می تواند به یک سیستم خودگردان تبدیل شود[ نیازمند منبع]
سیستم خودگردان سیستمی از معادلات دیفرانسیل معمولی است به این شکل
که x مقادیر را در فضای اقلیدسی n بُعدی می گیرد؛ t اغلب به عنوان زمان تعبیر می شود.
از سیستم معادلات دیفرانسیل شکلی متمایز می شود
که در آن قانون حاکم بر تکامل سیستم فقط به وضعیت فعلی سیستم بستگی ندارد بلکه به پارامتر t نیز بستگی دارد، که اغلب به عنوان زمان تفسیر می شود؛ چنین سیستم هایی بنا به تعریف خودگردان نیستند.
اجازه دهید x 1 ( t ) یک جواب منحصر به فرد از مسئله مقدار اولیه برای یک سیستم خودگردان باشد
سپس x 2 ( t ) = x 1 ( t − t 0 ) حل می کند
در واقع، نمایان گر s = t − t 0 ما داریم x 1 ( s ) = x 2 ( t ) و d s = d t ، بدین ترتیب
برای این شرایط اولیه، این اثبات بدیهی است،
سیستم های خودگردان را می توان با استفاده از فضای فاز به صورت کیفی تحلیل کرد. در حالت یک متغیره، این خط فاز است.
روش های زیر برای معادلات دیفرانسیل خودگردان یک بعدی اعمال می شود. هر معادله یک - بُعدی از مرتبه n برابر است با یک دستگاه مرتبه اول n - بُعدی ( همان طور که در معادله دیفرانسیل معمولی # کاهش به سیستم مرتبه اول شرح داده شده است ) ، اما لزوماً برعکس برقرار نیست.
معادله خودگردان مرتبه اول
جداشدنی است، بنابراین با مرتب سازی مجدد در فرم انتگرالی به راحتی قابل حل است
معادله خودگردان مرتبه دوم
دشوارتر است، اما با معرفی متغیر جدید می توان آن را حل کرد
و بیان مشتق دوم از x ( از طریق قاعده زنجیره ای ) به عنوان
به طوری که معادله اصلی شود


wiki: سیستم خودگردان (ریاضیات)
