سنجش فشرده یا حسگری فشرده به تکنیکِ پردازش سیگنال برای مخابرهٔ داده های بیشتر، با صرف هزینه کمتر گفته می شود. یکی از دغدغه های پژوهشگران حوزه مخابرات و پردازش سیگنال این است که بتوانند با صرف هزینه کمتر، اطلاعات بیشتری را مخابره نمایند. یکی از مسائلی که به این هدف کمک می کند؛ فشرده سازی اطلاعات است. یعنی به جای ارسال کامل اطلاعات، بخش زاید آن حذف و بخشی را که حاوی اطلاعات مفید یا شامل بخش عمده اطلاعات است ارسال می کنیم. یکی از راهکارهایی که برای فشرده سازی اطلاعات در سال های اخیر مطرح شده، مسئله سنجش فشرده است که مورد توجه فراوان محققین قرار گرفته است. با توجه به قضیه نایکوئیست برای بازیابی یک سیگنال نمونه برداری شده، نمونه برداری باید حداقل دو برابر پهنای باند سیگنال باشد. اما بعد از نمونه برداری برای ذخیره سازی یا ارسال سیگنال نمونه برداری شده به منظور فشرده سازی ناچار به دور ریختن بخشی از داده هستیم؛ بنابراین این ایده به ذهن می رسد که به جای نمونه برداری با نرخ بالا و سپس دور ریختن بخشی از داده پس از تبدیل به حوزهای دیگر ( DCT ) ، از همان اول عمل فشرده سازی و نمونه برداری را به صورت همزمان انجام دهیم. اینجاست که ایده سنجش فشرده مطرح می شود. [ ۱] [ ۲] [ ۳]
نمونه برداری فشرده[ ۴] [ ۵]
در سنجش فشرده به جای برداشتن نمونه از سیگنال، از سیگنال اندازه ( measure ) گرفته می شود. اندازه در واقع ترکیب خطی از چند نمونه است. تعداد اندازه گیری های مورد نیاز برای بازیابی سیگنال در سنجش فشرده به مراتب کمتر از تعداد نمونه های مورد نیاز برای بازیابی سیگنال طبق قضیه نایکوئیست است. در سنجش فشرده، هدف از اندازه گیری سیگنال با نرخ اطلاعاتی ( نرخی که به میزان اطلاعات یک سیگنال بستگی دارد ) آن و نه نمونه برداری با نرخ نایکوئیست و سپس بازیابی آن است. مثلاً یک سیگنال صوت با پهنای باند ۴ کیلوهرتز را در نظر بگیرید. با توجه به قضیه نایکوئیست برای بازیابی کامل این سیگنال نرخ نمونه برداری باید حداقل ۸ کیلوهرتز باشد، اما می دانیم سیگنال صورت در حوزه ( STFT ) [ ۶] تنک است، یعنی تعداد زیادی از ضرایب STFT آن صفر هستند. در نتیجه سیگنال صوتی در این حوزه به مراتب اطلاعات کمتری دارد پس می توانیم نرخ اندازه گیری را نسبت به نرخ نمونه برداری، متناسب با این کاهش حجم اطلاعات از حوزه زمان به حوزه STFT کاهش دهیم. در سنجش فشرده مدل مسئله به یک دستگاه فرومعین[ ۷] به صورت رابطه زیر تبدیل می شود و هدف پیدا کردن تنک ترین جواب این دستگاه معادلات فرومعین است.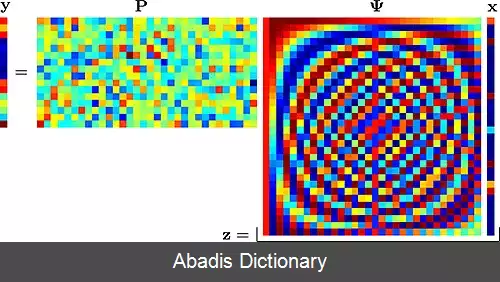
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفنمونه برداری فشرده[ ۴] [ ۵]
در سنجش فشرده به جای برداشتن نمونه از سیگنال، از سیگنال اندازه ( measure ) گرفته می شود. اندازه در واقع ترکیب خطی از چند نمونه است. تعداد اندازه گیری های مورد نیاز برای بازیابی سیگنال در سنجش فشرده به مراتب کمتر از تعداد نمونه های مورد نیاز برای بازیابی سیگنال طبق قضیه نایکوئیست است. در سنجش فشرده، هدف از اندازه گیری سیگنال با نرخ اطلاعاتی ( نرخی که به میزان اطلاعات یک سیگنال بستگی دارد ) آن و نه نمونه برداری با نرخ نایکوئیست و سپس بازیابی آن است. مثلاً یک سیگنال صوت با پهنای باند ۴ کیلوهرتز را در نظر بگیرید. با توجه به قضیه نایکوئیست برای بازیابی کامل این سیگنال نرخ نمونه برداری باید حداقل ۸ کیلوهرتز باشد، اما می دانیم سیگنال صورت در حوزه ( STFT ) [ ۶] تنک است، یعنی تعداد زیادی از ضرایب STFT آن صفر هستند. در نتیجه سیگنال صوتی در این حوزه به مراتب اطلاعات کمتری دارد پس می توانیم نرخ اندازه گیری را نسبت به نرخ نمونه برداری، متناسب با این کاهش حجم اطلاعات از حوزه زمان به حوزه STFT کاهش دهیم. در سنجش فشرده مدل مسئله به یک دستگاه فرومعین[ ۷] به صورت رابطه زیر تبدیل می شود و هدف پیدا کردن تنک ترین جواب این دستگاه معادلات فرومعین است.

wiki: سنجش فشرده
