سامانه لورنتس

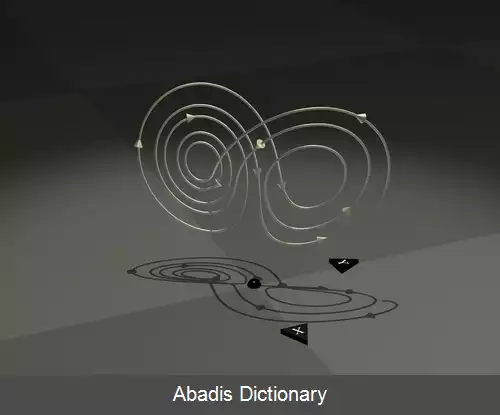
سیستم لورنز ( به انگلیسی: Lorenz system ) یک سیستم معادلات دیفرانسیل معمولی است که برای اولین بار توسط ادوارد لورنتس و الن فتر مورد بررسی قرار گرفت. برای داشتن راه حل های برای مقادیر خاص پارامتر و شرایط اولیه نظریه آشوب قابل توجه است. به شکل خاص، جاذب لورنتس مجموعه ای از راه حل های بی نظم سیستم لورنتس است. بر پایه مقالات منتشره در رسانه های مشهور، «اثر پروانه ای» از پیامدهای واقعی جاذب لورنتس ناشی می شود، یعنی در هر سیستم فیزیکی، در صورت عدم دانش کامل از شرایط اولیه ( حتی تغییرات کوچک هوا به دلیل بال زدن پروانه ) ، عملاً توانایی ما در پیش بینی مسیر آینده آن همیشه شکست خواهد خورد. در این سیستم تأکید می شود که سیستم های فیزیکی می توانند کاملاً قطعی باشند و در عین حال حتی در غیاب اثرات کوانتومی نیز ذاتاً قابل پیش بینی نباشند. شکل جاذب لورنتس نیز در صورت ترسیم گرافیکی، ممکن است شبیه یک پروانه باشد.
در سال ۱۹۶۳، ادوارد لورنتس، با کمک الن فتر، یک مدل ریاضی ساده برای همرفت جوی ایجاد کرد. [ ۱] این مدل سیستمی از سه معادله دیفرانسیل معمولی تشکیل شده است که اکنون به عنوان معادلات لورنتس شناخته می شوند:
معادلات لورنتس نیز در مدل های ساده شده برای لیزر، [ ۲] مولد الکتریکی، [ ۳] ترموسیفون، [ ۴] موتور جریان مستقیم، [ ۵] مدار الکتریکی، [ ۶] واکنش های شیمیایی[ ۷] و اسمز مستقیم کاربرد دارد. [ ۸] این معادلات همچنین از معادلات مطرح در فضای فوریه برای چرخ آب مالکوس هستند. [ ۹] [ ۱۰] چرخ آب مالکوس حرکت آشفته ای را به نمایش می گذارد که در آن به جای چرخش در یک جهت با سرعت ثابت، چرخشی با سرعت متناوب، کندی، توقف، تغییر جهت ها و نوسان به جلو و عقب یا ترکیبی از چنین رفتاری را به روشی غیرقابل پیش بینی دارد.
از نظر فنی، سیستم لورنتس غیرخطی، غیر دوره ای، سه بعدی و قطعی است. معادلات لورنتس موضوع صدها مقاله تحقیقاتی و حداقل یک کتاب بوده است. [ ۱۱]
به شکل پیش فرض پارامترها σ ، ρ ، و β مثبت هستند لورنتس از مقادیر σ = 10 ، β = 8 / 3 و ρ = 28 استفاده کرد. این سیستم رفتارهای آشفته ای را برای این مقادیر ( و نزدیک به آن ) نشان می دهد. [ ۱۲]
اگر ρ < 1 پس فقط یک نقطه تعادل وجود دارد که در مبدأ است. این نقطه با عدم همرفت مطابقت دارد. همه معادلات زمانی درست است، که عدد یک جاذب جهانی است ρ < 1 . [ ۱۳]